Significancia estadística y relevancia clínica
Índice de contenidos
Introducción
La realización de cualquier estudio clínico-epidemiológico pretende poner de manifiesto al final del mismo si existe o no asociación entre diferentes variables. Esta asociación puede ser resultado de que realmente exista la asociación indicada, pero esta asociación también puede ser producto del azar, de la presencia de sesgos o de la presencia de variables de confusión.
Una de las aplicaciones de la estadística es hacer inferencias a poblaciones, a partir de muestras. En la realización de este proceso inferencial, siempre existe el riesgo de error o imprecisión ya sea por el azar o la variabilidad biológica del fenómeno a estudiar. La carencia de error aleatorio debido al azar se conoce como precisión. Cuanto más grande es el tamaño muestral, mayor es la precisión y la variabilidad explicada por el azar disminuye. Esta posibilidad de error o falta de precisión, siempre que no existan sesgos o variables de confusión, se corrige aumentando el tamaño de la muestra. De cualquier manera el papel del azar debe ser siempre contemplado, evaluado y medido, realizando test de hipótesis o construyendo intervalos de confianza para conocer la precisión de nuestra estimación dentro de una seguridad previamente definida.
Desde el punto de vista clínico la significación estadística no resuelve todos los interrogantes que hay que responder ya que la asociación estadísticamente significativa puede no ser clínicamente relevante y además la asociación estadísticamente significativa puede no ser causal. En definitiva podemos encontrar asociaciones "estadísticamente posibles y conceptualmente estériles" .
Significación estadística
A pesar de las limitaciones de la estadística, el término "estadísticamente significativo" invade la literatura médica y se percibe como una etiqueta que indicase "garantía de calidad". El considerar el término significativo implica utilizar términos comparativos de dos hipótesis. Los test de hipótesis son test de significación estadística que cuantifican hasta que punto la variabilidad de la muestra puede ser responsable de los resultados de un estudio en particular. La Ho (hipótesis nula) representa la afirmación de que no hay asociación entre las dos variables estudiadas y la Ha (hipótesis alternativa) afirma que hay algún grado de relación o asociación entre las dos variables. Nuevamente la estadística nos muestra su utilidad ya que nos ayuda a tomar la decisión de que hipótesis debemos elegir. Dicha decisión puede ser afirmada con una seguridad que nosotros previamente decidimos. El nivel de significación se estableció siguiendo los comentarios del estadístico Fisher que señaló "...es conveniente trazar una línea de demarcación a partir de la cual podamos decir: o bien hay algo en el tratamiento..." . El mecanismo de los diferentes test se realiza aunque con matices siempre de la siguiente forma: En primer lugar se mira la magnitud de la diferencia que hay entre los grupos a comparar (A y B). Si esta magnitud o valor absoluto es mayor que un error estándar definido multiplicado por una seguridad definida, concluimos que la diferencia es significativa entre A y B. Por tanto aceptamos la hipótesis alternativa y rechazamos la hipótesis nula.
Ejemplo:
Disponemos de 2 tratamientos ( A y B). El tratamiento A lo reciben 25 pacientes y el tratamiento B otros 25 pacientes. 15 pacientes responden favorablemente al tratamiento A y 20 al tratamiento B. ¿Existe diferencia significativa entre ambos tratamientos?
Ho (hipótesis nula) = No hay diferencia entre ambos tratamientos.
Ha (hipótesis alternativa) = Sí existe diferencia.
| Tratamiento | N | Porcentaje de respuesta |
|---|---|---|
| A | 25 | 15/25 = 0.60 |
| B | 25 | 20/25 = 0.80 |
| Si |
|
es mayor que el producto de 1.96 * el error estándar, |
| concluímos que la diferencia es significativa. | ||
![]()
![]()
![]()
| Error estándar = |
|
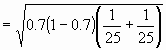 |
= 0.1296 |
Error estándar * 1.96 = 0.1296 * 1.96 = 0.25
| Como quiera que la diferencia = |
|
|
| no supera el valor 0.25 concluimos que la diferencia entre 0.60 y 0.80 no es estadísticamente significativa. A la vista de los resultados no podemos aceptar la Ha (hipótesis alternativa). |
El proceso de aceptación o rechazo de la hipótesis lleva implícito un riesgo que se cuantifica con el valor de la "p", que es la probabilidad de aceptar la hipótesis alternativa como cierta, cuando la cierta podría ser la hipótesis nula.
El valor de "p" que indica que la asociación es estadísticamente significativa ha sido arbitrariamente seleccionado y por consenso se considera en 0.05. Una seguridad del 95% lleva implícito una p < de 0.05 y una seguridad del 99% lleva implícita una p < 0.01. Cuando rechazamos la Ho(hipótesis nula) y aceptamos la Ha (hipótesis alternativa) como probablemente cierta afirmando que hay una asociación, o que hay diferencia, estamos diciendo en otras palabras que es muy poco probable que el azar fuese responsable de dicha asociación. Del mismo modo si la p>0.05 decimos que el azar no puede ser excluido como explicación de dicho hallazgo y no rechazamos la Ho (hipótesis nula) que afirma que ambas variables no están asociadas o correlacionadas.
Conviene por otra parte considerar que la significación estadística entre dos variables depende de dos componentes fundamentales. El primero es la magnitud de la diferencia a testar. Cuanto más grande sea la diferencia entre las dos variables, más fácil es demostrar que la diferencia es significativa. Por el contrario si la diferencia entre ambas variables es pequeña, las posibilidades de detectar diferencias entre las mismas se dificulta. El segundo componente fundamental a tener en cuanta al testar diferencias entre dos variables es el tamaño muestral. Cuanto más grande sea dicho tamaño muestral más fácil es detectar diferencias entre las mismas. Pequeñas diferencias se pueden detectar con grandes tamaños muestrales y grandes diferencias entre variables necesitan muchos menos pacientes o individuos a ser estudiados. Cualquier diferencia puede ser estadísticamente significativa si se dispone del suficiente número de pacientes.
Ejemplo:
En el ejemplo anterior objetivamos que no hay diferencia entre 60% y 80%. Supongamos que realizamos ahora el estudio con 900 pacientes en cada grupo:
| Si |
|
es mayor que el producto de 1.96 * el error estándar, |
| concluimos que la diferencia es significativa. | ||
![]()
![]()
![]()
| Error estándar = |
|
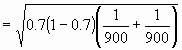 |
= 0.0216 |
Error estándar * 1.96 = 0.0216 * 1.96 = 0.042
| Como quiera que la diferencia = |
|
|
|
supera el valor 0.0423 concluimos que la diferencia entre 0.60 y 0.80 sí es estadísticamente significativa. A la vista de los resultados por tanto rechazamos la Ho (hipótesis nula) y aceptamos la Ha (hipótesis alternativa) como probablemente cierta. Como podemos objetivar en este segundo ejemplo ahora, si podemos decir que la diferencia entre 60% y 80% es estadísticamente significativa (p< 0.05). |
El tamaño muestral afecta a la probabilidad de la significación estadística a través del error estándar que se hace más pequeño cuantos más pacientes tenga el estudio. Así pues el valor de la "p" es función de la magnitud de la diferencia entre los dos grupos o dos variables y del tamaño de la muestra. Por esta razón una pequeña diferencia puede ser estadísticamente significativa si disponemos de un tamaño muestral lo suficientemente grande y por el contrario un efecto o diferencia relativamente grande puede no alcanzar la significación estadística si la variabilidad es grande debida a un pequeño tamaño muestral. Por estas razones los valores de la "p" deben ser considerados solo como una guía y no como base de conclusiones definitivas e irrevocables.
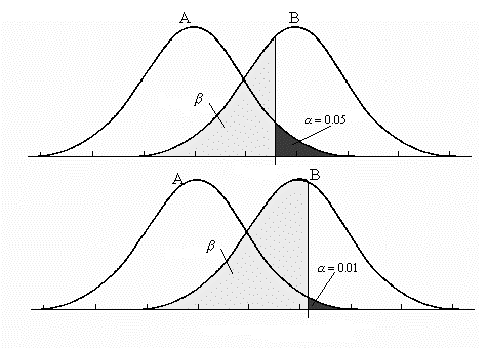
Al realizar el test estadístico, podríamos correr el riesgo de equivocarnos al rechazar la hipótesis nula. La probabilidad de rechazar la hipótesis nula cuando en realidad es verdadera (error de tipo I) se le denomina nivel de significación y es la "p". Esta probabilidad de rechazar la hipótesis nula cuando es verdadera se le conoce también como error alfa. La "p" no es por tanto un indicador de fuerza de la asociación ni de su importancia.
La significación estadística es por tanto una condición resultante del rechazo de una hipótesis nula mediante la aplicación de una prueba estadística de significación. El nivel de significación es el riesgo o la probabilidad que voluntariamente asume el investigador de equivocarse al rechazar la hipótesis nula, cuando en realidad es cierta. Este riesgo se establece normalmente en 0.05 ó 0.01.
El proceso de poner a prueba una hipótesis involucra una toma de decisiones para rechazar o no la hipótesis nula. Aunque los valores de la "p" son los de una variable continua, se utiliza para forzar una decisión cualitativa, tomando partido por una u otra hipótesis. Si p < 0.05 se considera significativo, en cuyo caso se rechaza la hipótesis nula y no significativo si p> 0.05 en cuyo caso no se rechaza. Una "p" pequeña significa que la probabilidad de que los resultados obtenidos se deban al azar es pequeña. Los sinónimos de la expresión estadísticamente significativos se muestran en la Tabla 1
El riesgo alfa α ("p") indica la probabilidad de cometer un error de tipo I (falso positivo). El error de tipo I, es por lo tanto rechazar la Ho cuando en realidad es verdadera. Se podría considerar que para evitar este tipo de error deberíamos de elegir un nivel de confianza más elevado, sin embargo al aumentar el nivel de confianza aumenta la probabilidad de cometer el error de tipo II. El error de tipo II consiste en aceptar la hipótesis nula cuando es falsa y esto se conoce como el error de tipo II o Beta (β ) (falso negativo) (Tabla 2).
En la ejecución de un estudio determinado no es posible saber si estamos cometiendo el error de tipo I o error de tipo II, sin embargo hay una serie de recomendaciones que podríamos seguir para disminuir dichos errores.
Recomendaciones para disminuir el error de tipo I:
- Disponer de una teoría que guíe la investigación, evitando el "salir de pesca" con el ordenador buscando asociaciones entre variables.
- Disminuir el número de test estadísticos llevados a cabo en el estudio.
- Depurar la base de datos para evitar errores de valores extremos que puedan producir hallazgos significativos.
- Utilizar valores de alfa más reducidos (0.01 ó 0.001).
- Reproducir el estudio. Si al reproducir el estudio se obtienen resultados similares, estaremos más seguros de no estar cometiendo el error de tipo I.
Recomendaciones para disminuir el error de tipo II:
- Incrementar el tamaño de la muestra.
- Estimar el poder estadístico del estudio.
- Incrementar el tamaño del efecto a detectar.
- Incrementar el valor de alfa.
- Utilizar test paramétricos (más potentes) en lugar de test no paramétricos.
Relevancia clínica
La relevancia clínica de un fenómeno va más allá de cálculos aritméticos y está determinada por el juicio clínico. La relevancia depende de la magnitud de la diferencia, la gravedad del problema a investigar, la vulnerabilidad, la morbimortalidad generada por el mismo, su coste y por su frecuencia entre otros elementos.
La reducción relativa del riesgo relativo es una medida de utilidad en el cálculo de la relevancia clínica. Reducciones del riesgo relativo de 50% casi siempre y de 25% con frecuencia, son consideradas como clínicamente relevantes independientemente de la significación estadística.
La práctica de la medicina basada en la evidencia considera el ensayo clínico aleatorizado como el estándar para valorar la eficacia de las tecnologías sanitarias y recomienda que las decisiones se tomen, siempre que se pueda, con opciones diagnósticas o terapéuticas de demostrada eficacia .
La forma recomendada de presentar los resultados de un ensayo clínico aleatorizado y otros tipos de estudio debe incluir: La reducción relativa del riesgo (RRR), la reducción absoluta del riesgo (RAR) y el número necesario de pacientes a tratar para reducir un evento (NNT). Consideremos para su cálculo este ejemplo: Mueren 15% de pacientes en el grupo de intervención y mueren un 20% en el grupo control. El que la diferencia entre ambos sea significativa dependerá del tamaño muestral. El riesgo relativo, que es el cociente entre los expuestos al nuevo tratamiento o actividad preventiva y los no expuestos, es en este caso (0.15/0.20=0.75). El riesgo de muerte de los pacientes que reciben el nuevo tratamiento relativo al de los pacientes del grupo control fue de 0.75. La RRR es el complemento del RR, es decir, (1-0.75)* 100 = 25%. El nuevo tratamiento reduce el riesgo de muerte en un 25% relativo al que ha ocurrido en el grupo control. La reducción absoluta del riesgo (RAR) sería: 0.20-0.15= 0.05 (5%). Podríamos decir por tanto que de cada 100 personas tratadas con el nuevo tratamiento podemos evitar 5 casos de muerte. La siguiente pregunta sería: si de cada 100 personas tratadas con el nuevo tratamiento podemos evitar 5 casos de muerte. ¿Cuántos tendríamos que tratar para evitar un solo caso de muerte?. En otras palabras ¿cuál es el NNT?. Su cálculo requiere una simple regla de tres que se resuelve dividiendo 1/RAR. En este caso 1/0.05 = 20. Por tanto la respuesta es que necesitamos tratar a 20 pacientes con el nuevo tratamiento para evitar un caso de muerte.
Este modo de presentar los resultados nos cuantifica el esfuerzo a realizar para conseguir la reducción de un evento desfavorable. El presentar los resultados sólo como reducción porcentual del riesgo relativo (RRR), aunque es técnicamente correcto, tiende a magnificar el efecto de la intervención al describir del mismo modo situaciones muy dispares. Dicho efecto lo podemos objetivar en la tabla 3, donde se objetiva que la reducción del riesgo es igual pero el NNT es completamente diferente. Cambios pequeños en el riesgo basal absoluto de un hecho clínico infrecuente conducen a grandes cambios en el número de pacientes que necesitamos tratar con la intención de prevenir uno.
El cálculo del NNT representa como ya hemos indicado el número de pacientes a tratar de manera experimental a fin de evitar que uno de ellos desarrolle un resultado negativo. Es por tanto una forma excelente de determinar la significación clínica de un ensayo que además sea estadísticamente significativo. Cuanto más reducido es NNT el efecto de la magnitud del tratamiento es mayor. Si no se encontrase eficacia en el tratamiento la reducción absoluta del riesgo sería cero y el NNT sería infinito. Como sucede en las estimaciones de otros parámetros, se debe expresar el NNT con intervalos de confianza para estimar la incertidumbre que dicho parámetro presenta.
El test de significación estadística nos proporciona una "p" que nos permiten conocer la probabilidad de equivocarse si rechazamos la Ho, pero es evidente que la relevancia del fenómeno a estudiar es un elemento clave en la toma de decisiones. Por otro lado aún siendo estadísticamente significativo y clínicamente relevante no debemos olvidar que antes de poner en marcha una practica clínica debemos a su vez valorar la validez externa o generalización de los resultados al universo de pacientes que se pretende aplicar dicha práctica clínica.
Cálculos online
Más
Bibliografía
- Wassertheil-Smoller S. Biostatistics and Epidemiology. A primer for health professionals. Second edition. New York: Springer-Verlag; 1995.
- Silva Ayçaguer LC. Cultura estadística e investigación científica en el campo de la salud: una mirada crítica. Madrid: Díaz de Santos; 1997.
- Fisher R. The design of experiments. Londres: Oliver and Boyd; 1935.
- Jekel JF, Elmore JG, Katz DL. Epidemiology Biostatistics and Preventive Medicine.Philadelphia: W.B. Saunders Company; 1996.
- Daly L.E, Bourke G.J. Interpretation and Uses of Medical Statistics. Oxford: Blackwell Science Ltd; 2000.
- Daly LE, Bourke GJ. Interpretation and uses of medical statistics. 5th ed.. Oxford: Blackwell science; 2000.
- Sackett DL, Haynes RB , Guyatt GH, Tugwell P. Epidemiología clínica. Ciencias básicas para la medicina clínica, 2ª ed. Madrid: Editorial Médica Panamericana; 1994.
- Sackett DL, Richarson WS, Rosenberg W, Hynes RB. Evidence-based medicine: how to practice and teach EBM. 2nd ed. London: Churchill-livingstone; 2000.
- Guyatt GH, Sackett DL, Cook DJ. Users´guides to the medical literature. II. How to use an articie about therapy or prevention. A. Are the results of the study valid? Evidence-Based Medicine Working Group. JAMA 1993; 270: 2598-2601.
- Laupacis A, Sackett DL, Roberts RS: An assesment of clinically useful measures of treatment. N Engl J Med 1988; 318: 1728-1733.
- Guyatt GH, Sackett DL, Cook DJ. Users´ guides to the medical literature. II. How to use an article about therapy or prevention. B. What were the results and will they help in caring for my patients? Evidence Based Medicine Working Group. JAMA 1994; 271: 59-63. [Medline]
- Cook RJ, Sackett DL. The number needed to treal: a clincally useful measure of treatment effect. BMJ 1995; 310: 452-454. [Texto completo]
- Altman DG. Confidence intervals for the nember needed to treat. BMJ 1998; 317: 1309-1312. [Texto completo]
- Daly LE. Confidence limits made easy: interval estimation using a subsitution method. Am J Epidemiol 1998; 147: 783-90. [Medline]
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 2001; 8: 191-195.
Significancia estadística y relevancia clínica
Índice de contenidos
Introducción
La realización de cualquier estudio clínico-epidemiológico pretende poner de manifiesto al final del mismo si existe o no asociación entre diferentes variables. Esta asociación puede ser resultado de que realmente exista la asociación indicada, pero esta asociación también puede ser producto del azar, de la presencia de sesgos o de la presencia de variables de confusión.
Una de las aplicaciones de la estadística es hacer inferencias a poblaciones, a partir de muestras. En la realización de este proceso inferencial, siempre existe el riesgo de error o imprecisión ya sea por el azar o la variabilidad biológica del fenómeno a estudiar. La carencia de error aleatorio debido al azar se conoce como precisión. Cuanto más grande es el tamaño muestral, mayor es la precisión y la variabilidad explicada por el azar disminuye. Esta posibilidad de error o falta de precisión, siempre que no existan sesgos o variables de confusión, se corrige aumentando el tamaño de la muestra. De cualquier manera el papel del azar debe ser siempre contemplado, evaluado y medido, realizando test de hipótesis o construyendo intervalos de confianza para conocer la precisión de nuestra estimación dentro de una seguridad previamente definida.
Desde el punto de vista clínico la significación estadística no resuelve todos los interrogantes que hay que responder ya que la asociación estadísticamente significativa puede no ser clínicamente relevante y además la asociación estadísticamente significativa puede no ser causal. En definitiva podemos encontrar asociaciones "estadísticamente posibles y conceptualmente estériles" .
Significación estadística
A pesar de las limitaciones de la estadística, el término "estadísticamente significativo" invade la literatura médica y se percibe como una etiqueta que indicase "garantía de calidad". El considerar el término significativo implica utilizar términos comparativos de dos hipótesis. Los test de hipótesis son test de significación estadística que cuantifican hasta que punto la variabilidad de la muestra puede ser responsable de los resultados de un estudio en particular. La Ho (hipótesis nula) representa la afirmación de que no hay asociación entre las dos variables estudiadas y la Ha (hipótesis alternativa) afirma que hay algún grado de relación o asociación entre las dos variables. Nuevamente la estadística nos muestra su utilidad ya que nos ayuda a tomar la decisión de que hipótesis debemos elegir. Dicha decisión puede ser afirmada con una seguridad que nosotros previamente decidimos. El nivel de significación se estableció siguiendo los comentarios del estadístico Fisher que señaló "...es conveniente trazar una línea de demarcación a partir de la cual podamos decir: o bien hay algo en el tratamiento..." . El mecanismo de los diferentes test se realiza aunque con matices siempre de la siguiente forma: En primer lugar se mira la magnitud de la diferencia que hay entre los grupos a comparar (A y B). Si esta magnitud o valor absoluto es mayor que un error estándar definido multiplicado por una seguridad definida, concluimos que la diferencia es significativa entre A y B. Por tanto aceptamos la hipótesis alternativa y rechazamos la hipótesis nula.
Ejemplo:
Disponemos de 2 tratamientos ( A y B). El tratamiento A lo reciben 25 pacientes y el tratamiento B otros 25 pacientes. 15 pacientes responden favorablemente al tratamiento A y 20 al tratamiento B. ¿Existe diferencia significativa entre ambos tratamientos?
Ho (hipótesis nula) = No hay diferencia entre ambos tratamientos.
Ha (hipótesis alternativa) = Sí existe diferencia.
| Tratamiento | N | Porcentaje de respuesta |
|---|---|---|
| A | 25 | 15/25 = 0.60 |
| B | 25 | 20/25 = 0.80 |
| Si |
|
es mayor que el producto de 1.96 * el error estándar, |
| concluímos que la diferencia es significativa. | ||
![]()
![]()
![]()
| Error estándar = |
|
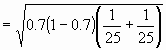 |
= 0.1296 |
Error estándar * 1.96 = 0.1296 * 1.96 = 0.25
| Como quiera que la diferencia = |
|
|
| no supera el valor 0.25 concluimos que la diferencia entre 0.60 y 0.80 no es estadísticamente significativa. A la vista de los resultados no podemos aceptar la Ha (hipótesis alternativa). |
El proceso de aceptación o rechazo de la hipótesis lleva implícito un riesgo que se cuantifica con el valor de la "p", que es la probabilidad de aceptar la hipótesis alternativa como cierta, cuando la cierta podría ser la hipótesis nula.
El valor de "p" que indica que la asociación es estadísticamente significativa ha sido arbitrariamente seleccionado y por consenso se considera en 0.05. Una seguridad del 95% lleva implícito una p < de 0.05 y una seguridad del 99% lleva implícita una p < 0.01. Cuando rechazamos la Ho(hipótesis nula) y aceptamos la Ha (hipótesis alternativa) como probablemente cierta afirmando que hay una asociación, o que hay diferencia, estamos diciendo en otras palabras que es muy poco probable que el azar fuese responsable de dicha asociación. Del mismo modo si la p>0.05 decimos que el azar no puede ser excluido como explicación de dicho hallazgo y no rechazamos la Ho (hipótesis nula) que afirma que ambas variables no están asociadas o correlacionadas.
Conviene por otra parte considerar que la significación estadística entre dos variables depende de dos componentes fundamentales. El primero es la magnitud de la diferencia a testar. Cuanto más grande sea la diferencia entre las dos variables, más fácil es demostrar que la diferencia es significativa. Por el contrario si la diferencia entre ambas variables es pequeña, las posibilidades de detectar diferencias entre las mismas se dificulta. El segundo componente fundamental a tener en cuanta al testar diferencias entre dos variables es el tamaño muestral. Cuanto más grande sea dicho tamaño muestral más fácil es detectar diferencias entre las mismas. Pequeñas diferencias se pueden detectar con grandes tamaños muestrales y grandes diferencias entre variables necesitan muchos menos pacientes o individuos a ser estudiados. Cualquier diferencia puede ser estadísticamente significativa si se dispone del suficiente número de pacientes.
Ejemplo:
En el ejemplo anterior objetivamos que no hay diferencia entre 60% y 80%. Supongamos que realizamos ahora el estudio con 900 pacientes en cada grupo:
| Si |
|
es mayor que el producto de 1.96 * el error estándar, |
| concluimos que la diferencia es significativa. | ||
![]()
![]()
![]()
| Error estándar = |
|
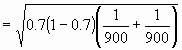 |
= 0.0216 |
Error estándar * 1.96 = 0.0216 * 1.96 = 0.042
| Como quiera que la diferencia = |
|
|
|
supera el valor 0.0423 concluimos que la diferencia entre 0.60 y 0.80 sí es estadísticamente significativa. A la vista de los resultados por tanto rechazamos la Ho (hipótesis nula) y aceptamos la Ha (hipótesis alternativa) como probablemente cierta. Como podemos objetivar en este segundo ejemplo ahora, si podemos decir que la diferencia entre 60% y 80% es estadísticamente significativa (p< 0.05). |
El tamaño muestral afecta a la probabilidad de la significación estadística a través del error estándar que se hace más pequeño cuantos más pacientes tenga el estudio. Así pues el valor de la "p" es función de la magnitud de la diferencia entre los dos grupos o dos variables y del tamaño de la muestra. Por esta razón una pequeña diferencia puede ser estadísticamente significativa si disponemos de un tamaño muestral lo suficientemente grande y por el contrario un efecto o diferencia relativamente grande puede no alcanzar la significación estadística si la variabilidad es grande debida a un pequeño tamaño muestral. Por estas razones los valores de la "p" deben ser considerados solo como una guía y no como base de conclusiones definitivas e irrevocables.
Al realizar el test estadístico, podríamos correr el riesgo de equivocarnos al rechazar la hipótesis nula. La probabilidad de rechazar la hipótesis nula cuando en realidad es verdadera (error de tipo I) se le denomina nivel de significación y es la "p". Esta probabilidad de rechazar la hipótesis nula cuando es verdadera se le conoce también como error alfa. La "p" no es por tanto un indicador de fuerza de la asociación ni de su importancia.
La significación estadística es por tanto una condición resultante del rechazo de una hipótesis nula mediante la aplicación de una prueba estadística de significación. El nivel de significación es el riesgo o la probabilidad que voluntariamente asume el investigador de equivocarse al rechazar la hipótesis nula, cuando en realidad es cierta. Este riesgo se establece normalmente en 0.05 ó 0.01.
El proceso de poner a prueba una hipótesis involucra una toma de decisiones para rechazar o no la hipótesis nula. Aunque los valores de la "p" son los de una variable continua, se utiliza para forzar una decisión cualitativa, tomando partido por una u otra hipótesis. Si p < 0.05 se considera significativo, en cuyo caso se rechaza la hipótesis nula y no significativo si p> 0.05 en cuyo caso no se rechaza. Una "p" pequeña significa que la probabilidad de que los resultados obtenidos se deban al azar es pequeña. Los sinónimos de la expresión estadísticamente significativos se muestran en la Tabla 1
El riesgo alfa α ("p") indica la probabilidad de cometer un error de tipo I (falso positivo). El error de tipo I, es por lo tanto rechazar la Ho cuando en realidad es verdadera. Se podría considerar que para evitar este tipo de error deberíamos de elegir un nivel de confianza más elevado, sin embargo al aumentar el nivel de confianza aumenta la probabilidad de cometer el error de tipo II. El error de tipo II consiste en aceptar la hipótesis nula cuando es falsa y esto se conoce como el error de tipo II o Beta (β ) (falso negativo) (Tabla 2).
En la ejecución de un estudio determinado no es posible saber si estamos cometiendo el error de tipo I o error de tipo II, sin embargo hay una serie de recomendaciones que podríamos seguir para disminuir dichos errores.
Recomendaciones para disminuir el error de tipo I:
- Disponer de una teoría que guíe la investigación, evitando el "salir de pesca" con el ordenador buscando asociaciones entre variables.
- Disminuir el número de test estadísticos llevados a cabo en el estudio.
- Depurar la base de datos para evitar errores de valores extremos que puedan producir hallazgos significativos.
- Utilizar valores de alfa más reducidos (0.01 ó 0.001).
- Reproducir el estudio. Si al reproducir el estudio se obtienen resultados similares, estaremos más seguros de no estar cometiendo el error de tipo I.
Recomendaciones para disminuir el error de tipo II:
- Incrementar el tamaño de la muestra.
- Estimar el poder estadístico del estudio.
- Incrementar el tamaño del efecto a detectar.
- Incrementar el valor de alfa.
- Utilizar test paramétricos (más potentes) en lugar de test no paramétricos.
Relevancia clínica
La relevancia clínica de un fenómeno va más allá de cálculos aritméticos y está determinada por el juicio clínico. La relevancia depende de la magnitud de la diferencia, la gravedad del problema a investigar, la vulnerabilidad, la morbimortalidad generada por el mismo, su coste y por su frecuencia entre otros elementos.
La reducción relativa del riesgo relativo es una medida de utilidad en el cálculo de la relevancia clínica. Reducciones del riesgo relativo de 50% casi siempre y de 25% con frecuencia, son consideradas como clínicamente relevantes independientemente de la significación estadística.
La práctica de la medicina basada en la evidencia considera el ensayo clínico aleatorizado como el estándar para valorar la eficacia de las tecnologías sanitarias y recomienda que las decisiones se tomen, siempre que se pueda, con opciones diagnósticas o terapéuticas de demostrada eficacia .
La forma recomendada de presentar los resultados de un ensayo clínico aleatorizado y otros tipos de estudio debe incluir: La reducción relativa del riesgo (RRR), la reducción absoluta del riesgo (RAR) y el número necesario de pacientes a tratar para reducir un evento (NNT). Consideremos para su cálculo este ejemplo: Mueren 15% de pacientes en el grupo de intervención y mueren un 20% en el grupo control. El que la diferencia entre ambos sea significativa dependerá del tamaño muestral. El riesgo relativo, que es el cociente entre los expuestos al nuevo tratamiento o actividad preventiva y los no expuestos, es en este caso (0.15/0.20=0.75). El riesgo de muerte de los pacientes que reciben el nuevo tratamiento relativo al de los pacientes del grupo control fue de 0.75. La RRR es el complemento del RR, es decir, (1-0.75)* 100 = 25%. El nuevo tratamiento reduce el riesgo de muerte en un 25% relativo al que ha ocurrido en el grupo control. La reducción absoluta del riesgo (RAR) sería: 0.20-0.15= 0.05 (5%). Podríamos decir por tanto que de cada 100 personas tratadas con el nuevo tratamiento podemos evitar 5 casos de muerte. La siguiente pregunta sería: si de cada 100 personas tratadas con el nuevo tratamiento podemos evitar 5 casos de muerte. ¿Cuántos tendríamos que tratar para evitar un solo caso de muerte?. En otras palabras ¿cuál es el NNT?. Su cálculo requiere una simple regla de tres que se resuelve dividiendo 1/RAR. En este caso 1/0.05 = 20. Por tanto la respuesta es que necesitamos tratar a 20 pacientes con el nuevo tratamiento para evitar un caso de muerte.
Este modo de presentar los resultados nos cuantifica el esfuerzo a realizar para conseguir la reducción de un evento desfavorable. El presentar los resultados sólo como reducción porcentual del riesgo relativo (RRR), aunque es técnicamente correcto, tiende a magnificar el efecto de la intervención al describir del mismo modo situaciones muy dispares. Dicho efecto lo podemos objetivar en la tabla 3, donde se objetiva que la reducción del riesgo es igual pero el NNT es completamente diferente. Cambios pequeños en el riesgo basal absoluto de un hecho clínico infrecuente conducen a grandes cambios en el número de pacientes que necesitamos tratar con la intención de prevenir uno.
El cálculo del NNT representa como ya hemos indicado el número de pacientes a tratar de manera experimental a fin de evitar que uno de ellos desarrolle un resultado negativo. Es por tanto una forma excelente de determinar la significación clínica de un ensayo que además sea estadísticamente significativo. Cuanto más reducido es NNT el efecto de la magnitud del tratamiento es mayor. Si no se encontrase eficacia en el tratamiento la reducción absoluta del riesgo sería cero y el NNT sería infinito. Como sucede en las estimaciones de otros parámetros, se debe expresar el NNT con intervalos de confianza para estimar la incertidumbre que dicho parámetro presenta.
El test de significación estadística nos proporciona una "p" que nos permiten conocer la probabilidad de equivocarse si rechazamos la Ho, pero es evidente que la relevancia del fenómeno a estudiar es un elemento clave en la toma de decisiones. Por otro lado aún siendo estadísticamente significativo y clínicamente relevante no debemos olvidar que antes de poner en marcha una practica clínica debemos a su vez valorar la validez externa o generalización de los resultados al universo de pacientes que se pretende aplicar dicha práctica clínica.
Cálculos online
Más
Bibliografía
- Wassertheil-Smoller S. Biostatistics and Epidemiology. A primer for health professionals. Second edition. New York: Springer-Verlag; 1995.
- Silva Ayçaguer LC. Cultura estadística e investigación científica en el campo de la salud: una mirada crítica. Madrid: Díaz de Santos; 1997.
- Fisher R. The design of experiments. Londres: Oliver and Boyd; 1935.
- Jekel JF, Elmore JG, Katz DL. Epidemiology Biostatistics and Preventive Medicine.Philadelphia: W.B. Saunders Company; 1996.
- Daly L.E, Bourke G.J. Interpretation and Uses of Medical Statistics. Oxford: Blackwell Science Ltd; 2000.
- Daly LE, Bourke GJ. Interpretation and uses of medical statistics. 5th ed.. Oxford: Blackwell science; 2000.
- Sackett DL, Haynes RB , Guyatt GH, Tugwell P. Epidemiología clínica. Ciencias básicas para la medicina clínica, 2ª ed. Madrid: Editorial Médica Panamericana; 1994.
- Sackett DL, Richarson WS, Rosenberg W, Hynes RB. Evidence-based medicine: how to practice and teach EBM. 2nd ed. London: Churchill-livingstone; 2000.
- Guyatt GH, Sackett DL, Cook DJ. Users´guides to the medical literature. II. How to use an articie about therapy or prevention. A. Are the results of the study valid? Evidence-Based Medicine Working Group. JAMA 1993; 270: 2598-2601.
- Laupacis A, Sackett DL, Roberts RS: An assesment of clinically useful measures of treatment. N Engl J Med 1988; 318: 1728-1733.
- Guyatt GH, Sackett DL, Cook DJ. Users´ guides to the medical literature. II. How to use an article about therapy or prevention. B. What were the results and will they help in caring for my patients? Evidence Based Medicine Working Group. JAMA 1994; 271: 59-63. [Medline]
- Cook RJ, Sackett DL. The number needed to treal: a clincally useful measure of treatment effect. BMJ 1995; 310: 452-454. [Texto completo]
- Altman DG. Confidence intervals for the nember needed to treat. BMJ 1998; 317: 1309-1312. [Texto completo]
- Daly LE. Confidence limits made easy: interval estimation using a subsitution method. Am J Epidemiol 1998; 147: 783-90. [Medline]
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 2001; 8: 191-195.