Técnicas de regresión: Regresión Lineal Simple
Índice de contenidos
Introducción
En múltiples ocasiones en la práctica clínica nos encontramos con situaciones en las que se requiere analizar la relación entre dos variables cuantitativas. Los dos objetivos fundamentales de este análisis serán, por un lado, determinar si dichas variables están asociadas y en qué sentido se da dicha asociación (es decir, si los valores de una de las variables tienden a aumentar –o disminuir- al aumentar los valores de la otra); y por otro, estudiar si los valores de una variable pueden ser utilizados para predecir el valor de la otra.
La forma correcta de abordar el primer problema es recurriendo a coeficientes de correlación. Sin embargo, el estudio de la correlación es insuficiente para obtener una respuesta a la segunda cuestión: se limita a indicar la fuerza de la asociación mediante un único número, tratando las variables de modo simétrico, mientras que nosotros estaríamos interesados en modelizar dicha relación y usar una de las variables para explicar la otra. Para tal propósito se recurrirá a la técnica de regresión. Aquí analizaremos el caso más sencillo en el que se considera únicamente la relación entre dos variables. Así mismo, nos limitaremos al caso en el que la relación que se pretende modelizar es de tipo lineal.
La recta de regresión
Consideremos una variable aleatoria respuesta (o dependiente) Y, que supondremos relacionada con otra variable (no necesariamente aleatoria) que llamaremos explicativa, predictora o independiente y que se denotará por X. A partir de una muestra de n individuos para los que se dispone de los valores de ambas variables, {(Xi,Yi),i = 1,...n}, se puede visualizar gráficamente la relación existente entre ambas mediante un gráfico de dispersión, en el que los valores de la variable X se disponen en el eje horizontal y los de Y en el vertical. El problema que subyace a la metodología de la regresión lineal simple es el de encontrar una recta que ajuste a la nube de puntos del diagrama así dibujado, y que pueda ser utilizada para predecir los valores de Y a partir de los de X. La ecuación general de la recta de regresión será entonces de la forma: Y = a + bX .
El problema radica en encontrar aquella recta que mejor ajuste a los datos. Tradicionalmente se ha recurrido para ello al método de mínimos cuadrados, que elige como recta de regresión a aquella que minimiza las distancias verticales de las observaciones a la recta. Más concretamente, se pretende encontrar a y b tales que:
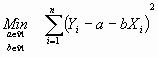
Resolviendo este problema mediante un sencillo cálculo de diferenciación, se obtienen los estimadores mínimo cuadráticos de los coeficientes de la recta de regresión:
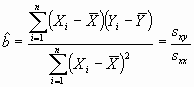 |
; |
|
La Tabla 1 muestra los datos de 69 pacientes de los que se conoce su edad y una medición de su tensión sistólica. Si estamos interesados en estudiar la variación en la tensión sistólica en función de la edad del individuo, deberemos considerar como variable respuesta la tensión y como variable predictora la edad. En la Figura 1 se muestra, superpuesta al diagrama de dispersión, la recta de regresión de mínimos cuadrados correspondientes, así como las distancias verticales de las observaciones muestrales a la recta. Aplicando los cálculos anteriores a este caso, resultaría:
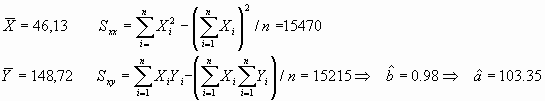
Como se puede suponer, la relación Y = a + bX no va a cumplirse exactamente, sino que existirá un error ![]() que representa la variación de Y en todos los datos con un mismo valor de la variable independiente. Las distancias verticales entre el valor observado y el valor dado por la recta para cada individuo (o valor ajustado) reciben el nombre de residuos, y se suelen denotar por
que representa la variación de Y en todos los datos con un mismo valor de la variable independiente. Las distancias verticales entre el valor observado y el valor dado por la recta para cada individuo (o valor ajustado) reciben el nombre de residuos, y se suelen denotar por ![]() . La expresión teórica del modelo matemático será, por tanto:
. La expresión teórica del modelo matemático será, por tanto:
![]()
| donde, además, se supondrá |
|
Interpretación de los coeficientes de regresión y tabla ANOVA
En la ecuación general de la recta de regresión, claramente b es la pendiente de la recta y a el valor de la variable dependiente Y para el que X = 0. En consecuencia, una vez estimados estos coeficientes, en la mayoría de las aplicaciones clínicas el valor de â no tendrá una interpretación directa, mientras que el valor ![]() servirá como un indicador del sentido de asociación entre ambas variables: así,
servirá como un indicador del sentido de asociación entre ambas variables: así, ![]() nos indicará una relación directa entre ellas (a mayor valor de la variable explicativa, el valor de la variable dependiente Y aumentará),
nos indicará una relación directa entre ellas (a mayor valor de la variable explicativa, el valor de la variable dependiente Y aumentará), ![]() delatará una relación de tipo inverso, mientras que
delatará una relación de tipo inverso, mientras que ![]() nos indica que no existe una relación lineal clara entre ambas variables. Así mismo, y tal y como se deduce de la ecuación de la recta de regresión, el coeficiente b nos da una estimación del cambio por término medio en la variable Y por cada unidad en que se incrementa X. Al igual que ocurre con otros estimadores, existirá cierta incertidumbre en el cálculo de las estimaciones, que se podrá reflejar mediante intervalos de confianza para ambos valores, construidos bajo la hipótesis de normalidad de los residuos, mediante las expresiones:
nos indica que no existe una relación lineal clara entre ambas variables. Así mismo, y tal y como se deduce de la ecuación de la recta de regresión, el coeficiente b nos da una estimación del cambio por término medio en la variable Y por cada unidad en que se incrementa X. Al igual que ocurre con otros estimadores, existirá cierta incertidumbre en el cálculo de las estimaciones, que se podrá reflejar mediante intervalos de confianza para ambos valores, construidos bajo la hipótesis de normalidad de los residuos, mediante las expresiones:
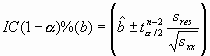
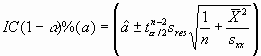
donde ![]() denota al cuantil de orden ß de una distribución t de Student con n-2 grados de libertad.
denota al cuantil de orden ß de una distribución t de Student con n-2 grados de libertad.
De igual forma, podemos limitar esta incertidumbre realizando un test para contrastar la hipótesis de que b=0 mediante el cociente ![]() y comparando éste con la distribución t de Student con n-2 grados de libertad. De modo análogo se llevaría a cabo un contraste para la hipótesis a=0. El hecho de que el test no resulte significativo indicará la ausencia de una relación clara de tipo lineal entre las variables, aunque pueda existir una asociación que no sea captada a través de una recta. Para los datos del ejemplo, el resultado de ajustar un modelo de regresión lineal se muestra en la Tabla 2.
y comparando éste con la distribución t de Student con n-2 grados de libertad. De modo análogo se llevaría a cabo un contraste para la hipótesis a=0. El hecho de que el test no resulte significativo indicará la ausencia de una relación clara de tipo lineal entre las variables, aunque pueda existir una asociación que no sea captada a través de una recta. Para los datos del ejemplo, el resultado de ajustar un modelo de regresión lineal se muestra en la Tabla 2.
La recta así ajustada explica tan sólo una parte de la variabilidad de la variable dependiente, expresada ésta comúnmente por medio de la varianza de Y, mientras que la cantidad de variabilidad que resta por explicar puede ser expresada a través de los residuos. Generalmente un análisis de regresión suele ser expresado por una tabla de análisis de la varianza en la que se refleja toda esta información. En la Tabla 2 se muestra además la tabla correspondiente en el ejemplo de la tensión sistólica. La columna etiquetada por "Suma de cuadrados" muestra una descomposición de la variación total de Y en las partes explicada y no explicada (residual) por la regresión. La proporción de variabilidad explicada por el modelo coincide aquí con el cuadrado del coeficiente de correlación lineal de Pearson, que recibe el nombre de coeficiente de determinación, y que se persigue sea próximo a 1. En nuestro ejemplo sería R2=0.645.
A partir de esta información puede elaborarse un contraste para verificar la utilidad del modelo. En el caso de regresión lineal simple, el estadístico de contraste se reduce a:
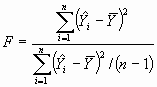
que se comparará con el cuantil correspondiente a una distribución F de Snedecor con parámetros 1 y n-1. El test resultante será equivalente al test t para contrastar H0:b=0.
Hipótesis del modelo
Una vez ajustado el modelo, y antes de usarlo para realizar nuevas predicciones, conviene asegurarse de que no se violan las hipótesis sobre las que se soporta: independencia de las observaciones muestrales, normalidad de los valores de la variable dependiente Y para cada valor de la variable explicativa, homocedasticidad (i.e., la variabilidad de Y es la misma para todos los valores de X) y relación lineal entre las dos variables. La información más relevante la aportan los residuos. Así, bajo las suposiciones anteriores, los residuos habrán de tener una distribución normal de media cero y varianza constante. El modo más sencillo de comprobar si esto se verifica es obteniendo una impresión visual a partir de un gráfico de los residuos frente a la variable dependiente Y. La Figura 2 muestra las diferentes posibilidades en un gráfico de residuos, mientras que el gráfico que se obtiene en el ejemplo manejado se refleja en la Figura 3.
Se puede complementar este análisis mediante gráficos de probabilidad normal y tests de normalidad para los residuos, como el de Kolmogorov-Smirnov (Figura 4). Así mismo, la independencia de las observaciones puede estudiarse mediante gráficos de autocorrelación y contrastes de independencia como el de Durbin-Watson.
Aunque obviaremos un análisis detallado de la verificación de las hipótesis del modelo, conviene hacer referencia a las medidas a tomar en caso de no cumplirse. Para el caso de no normalidad, resulta obvio que la medida más inmediata es la transformación de la variable dependiente, aunque otra alternativa son los cada vez más utilizados modelos de regresión no paramétrica, que evitan la suposición de una distribución gaussiana. También se debe modificar el modelo en el caso de datos dependientes o valores repetidos.
Predicción
Cuando se verifican las hipótesis sobre las que se asienta el modelo, la recta de regresión puede ser utilizada para predecir el valor medio de la variable Y para cada valor concreto de X. Calculando la esperanza matemática en ambos lados de la ecuación (1) se obtendrá:
![]()
de modo que la línea de regresión proporciona un estimador del valor medio de Y para cada valor de X. Como tal estimador, debemos considerar la incertidumbre asociada a esta recta, que puede ser reflejada mediante regiones de confianza que contienen a la recta. En la Figura 5 se muestra, superpuesta al diagrama de dispersión, la recta de regresión en el ejemplo de la tensión sistólica que estamos manejando, así como una región de confianza para la misma, que contendrá a la verdadera relación entre tensión sistólica y edad con una seguridad del 95%.
También se puede utilizar la recta de regresión como estimador del valor de Y en un individuo concreto. En este caso se esperará una mayor incertidumbre en la estimación que en el caso de predecir una tendencia media. En la Figura 4 se muestra además la banda de predicción para el ejemplo que estamos manejando, siendo ésta mucho más amplia que en el caso de intentar predecir el valor medio.
La regresión lineal simple es entonces una técnica sencilla y accesible para valorar la relación entre dos variables cuantitativas en la práctica clínica, proponiendo además un modelo al que se ajusta dicha relación. No debemos olvidar que a lo largo de este artículo hemos abordado el caso más sencillo en el que se obvia el problema de un número más elevado de variables entre las que valorar la relación. En este caso entraríamos de lleno en la temática de la regresión lineal múltiple, lo cual nos obligaría a abordar problemas de índole más complicado como el de la colinealidad, interacción entre variables, variables confusoras o un análisis más detallado de los residuos del modelo. Así mismo, no se debe pasar por alto el hecho de que en la mayoría de las aplicaciones prácticas la relación que se observa entre pares de variables no es tanto lineal como de tipo curvilíneo (ya sea una relación logarítmica, exponencial, polinómica, etc.). En estos casos, aunque se puede hablar de regresión curvilínea según el tipo de relación, una conveniente transformación de las variables reduce el problema al caso que acabamos de abordar.
Bibliografía
- Pita Fernández S, Rey Sierra T, Vila Alonso MT. Relaciones entre variables cuantitativas (I). Cadernos de Atención Primaria 1997; 4: 141-145.
- Seber GAF. Linear Regression Analysis. New York: John Wiley & Sons, 1977.
- Bland JM, Altman DG. Statistics Notes: Transforming data. BMJ 1996; 312:770. [Medline] [Texto completo]
- Härdle. Aplied Nonparametric Regression. Cambridge: University Press, 1990.
- Statistics notes: Correlation, regression and repeated data. BMJ 1994; 308: 896. [Texto completo]
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
- Etxebarría Murgiondo, J. Regresión Múltiple. Madrid: La Muralla; 1999.
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 2000; 7: 91-94
Técnicas de regresión: Regresión Lineal Simple
Índice de contenidos
Introducción
En múltiples ocasiones en la práctica clínica nos encontramos con situaciones en las que se requiere analizar la relación entre dos variables cuantitativas. Los dos objetivos fundamentales de este análisis serán, por un lado, determinar si dichas variables están asociadas y en qué sentido se da dicha asociación (es decir, si los valores de una de las variables tienden a aumentar –o disminuir- al aumentar los valores de la otra); y por otro, estudiar si los valores de una variable pueden ser utilizados para predecir el valor de la otra.
La forma correcta de abordar el primer problema es recurriendo a coeficientes de correlación. Sin embargo, el estudio de la correlación es insuficiente para obtener una respuesta a la segunda cuestión: se limita a indicar la fuerza de la asociación mediante un único número, tratando las variables de modo simétrico, mientras que nosotros estaríamos interesados en modelizar dicha relación y usar una de las variables para explicar la otra. Para tal propósito se recurrirá a la técnica de regresión. Aquí analizaremos el caso más sencillo en el que se considera únicamente la relación entre dos variables. Así mismo, nos limitaremos al caso en el que la relación que se pretende modelizar es de tipo lineal.
La recta de regresión
Consideremos una variable aleatoria respuesta (o dependiente) Y, que supondremos relacionada con otra variable (no necesariamente aleatoria) que llamaremos explicativa, predictora o independiente y que se denotará por X. A partir de una muestra de n individuos para los que se dispone de los valores de ambas variables, {(Xi,Yi),i = 1,...n}, se puede visualizar gráficamente la relación existente entre ambas mediante un gráfico de dispersión, en el que los valores de la variable X se disponen en el eje horizontal y los de Y en el vertical. El problema que subyace a la metodología de la regresión lineal simple es el de encontrar una recta que ajuste a la nube de puntos del diagrama así dibujado, y que pueda ser utilizada para predecir los valores de Y a partir de los de X. La ecuación general de la recta de regresión será entonces de la forma: Y = a + bX .
El problema radica en encontrar aquella recta que mejor ajuste a los datos. Tradicionalmente se ha recurrido para ello al método de mínimos cuadrados, que elige como recta de regresión a aquella que minimiza las distancias verticales de las observaciones a la recta. Más concretamente, se pretende encontrar a y b tales que:
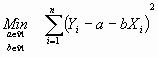
Resolviendo este problema mediante un sencillo cálculo de diferenciación, se obtienen los estimadores mínimo cuadráticos de los coeficientes de la recta de regresión:
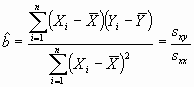 |
; |
|
La Tabla 1 muestra los datos de 69 pacientes de los que se conoce su edad y una medición de su tensión sistólica. Si estamos interesados en estudiar la variación en la tensión sistólica en función de la edad del individuo, deberemos considerar como variable respuesta la tensión y como variable predictora la edad. En la Figura 1 se muestra, superpuesta al diagrama de dispersión, la recta de regresión de mínimos cuadrados correspondientes, así como las distancias verticales de las observaciones muestrales a la recta. Aplicando los cálculos anteriores a este caso, resultaría:
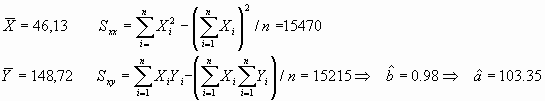
Como se puede suponer, la relación Y = a + bX no va a cumplirse exactamente, sino que existirá un error ![]() que representa la variación de Y en todos los datos con un mismo valor de la variable independiente. Las distancias verticales entre el valor observado y el valor dado por la recta para cada individuo (o valor ajustado) reciben el nombre de residuos, y se suelen denotar por
que representa la variación de Y en todos los datos con un mismo valor de la variable independiente. Las distancias verticales entre el valor observado y el valor dado por la recta para cada individuo (o valor ajustado) reciben el nombre de residuos, y se suelen denotar por ![]() . La expresión teórica del modelo matemático será, por tanto:
. La expresión teórica del modelo matemático será, por tanto:
![]()
| donde, además, se supondrá |
|
Interpretación de los coeficientes de regresión y tabla ANOVA
En la ecuación general de la recta de regresión, claramente b es la pendiente de la recta y a el valor de la variable dependiente Y para el que X = 0. En consecuencia, una vez estimados estos coeficientes, en la mayoría de las aplicaciones clínicas el valor de â no tendrá una interpretación directa, mientras que el valor ![]() servirá como un indicador del sentido de asociación entre ambas variables: así,
servirá como un indicador del sentido de asociación entre ambas variables: así, ![]() nos indicará una relación directa entre ellas (a mayor valor de la variable explicativa, el valor de la variable dependiente Y aumentará),
nos indicará una relación directa entre ellas (a mayor valor de la variable explicativa, el valor de la variable dependiente Y aumentará), ![]() delatará una relación de tipo inverso, mientras que
delatará una relación de tipo inverso, mientras que ![]() nos indica que no existe una relación lineal clara entre ambas variables. Así mismo, y tal y como se deduce de la ecuación de la recta de regresión, el coeficiente b nos da una estimación del cambio por término medio en la variable Y por cada unidad en que se incrementa X. Al igual que ocurre con otros estimadores, existirá cierta incertidumbre en el cálculo de las estimaciones, que se podrá reflejar mediante intervalos de confianza para ambos valores, construidos bajo la hipótesis de normalidad de los residuos, mediante las expresiones:
nos indica que no existe una relación lineal clara entre ambas variables. Así mismo, y tal y como se deduce de la ecuación de la recta de regresión, el coeficiente b nos da una estimación del cambio por término medio en la variable Y por cada unidad en que se incrementa X. Al igual que ocurre con otros estimadores, existirá cierta incertidumbre en el cálculo de las estimaciones, que se podrá reflejar mediante intervalos de confianza para ambos valores, construidos bajo la hipótesis de normalidad de los residuos, mediante las expresiones:
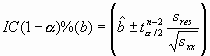
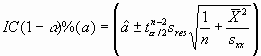
donde ![]() denota al cuantil de orden ß de una distribución t de Student con n-2 grados de libertad.
denota al cuantil de orden ß de una distribución t de Student con n-2 grados de libertad.
De igual forma, podemos limitar esta incertidumbre realizando un test para contrastar la hipótesis de que b=0 mediante el cociente ![]() y comparando éste con la distribución t de Student con n-2 grados de libertad. De modo análogo se llevaría a cabo un contraste para la hipótesis a=0. El hecho de que el test no resulte significativo indicará la ausencia de una relación clara de tipo lineal entre las variables, aunque pueda existir una asociación que no sea captada a través de una recta. Para los datos del ejemplo, el resultado de ajustar un modelo de regresión lineal se muestra en la Tabla 2.
y comparando éste con la distribución t de Student con n-2 grados de libertad. De modo análogo se llevaría a cabo un contraste para la hipótesis a=0. El hecho de que el test no resulte significativo indicará la ausencia de una relación clara de tipo lineal entre las variables, aunque pueda existir una asociación que no sea captada a través de una recta. Para los datos del ejemplo, el resultado de ajustar un modelo de regresión lineal se muestra en la Tabla 2.
La recta así ajustada explica tan sólo una parte de la variabilidad de la variable dependiente, expresada ésta comúnmente por medio de la varianza de Y, mientras que la cantidad de variabilidad que resta por explicar puede ser expresada a través de los residuos. Generalmente un análisis de regresión suele ser expresado por una tabla de análisis de la varianza en la que se refleja toda esta información. En la Tabla 2 se muestra además la tabla correspondiente en el ejemplo de la tensión sistólica. La columna etiquetada por "Suma de cuadrados" muestra una descomposición de la variación total de Y en las partes explicada y no explicada (residual) por la regresión. La proporción de variabilidad explicada por el modelo coincide aquí con el cuadrado del coeficiente de correlación lineal de Pearson, que recibe el nombre de coeficiente de determinación, y que se persigue sea próximo a 1. En nuestro ejemplo sería R2=0.645.
A partir de esta información puede elaborarse un contraste para verificar la utilidad del modelo. En el caso de regresión lineal simple, el estadístico de contraste se reduce a:
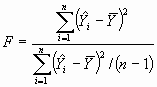
que se comparará con el cuantil correspondiente a una distribución F de Snedecor con parámetros 1 y n-1. El test resultante será equivalente al test t para contrastar H0:b=0.
Hipótesis del modelo
Una vez ajustado el modelo, y antes de usarlo para realizar nuevas predicciones, conviene asegurarse de que no se violan las hipótesis sobre las que se soporta: independencia de las observaciones muestrales, normalidad de los valores de la variable dependiente Y para cada valor de la variable explicativa, homocedasticidad (i.e., la variabilidad de Y es la misma para todos los valores de X) y relación lineal entre las dos variables. La información más relevante la aportan los residuos. Así, bajo las suposiciones anteriores, los residuos habrán de tener una distribución normal de media cero y varianza constante. El modo más sencillo de comprobar si esto se verifica es obteniendo una impresión visual a partir de un gráfico de los residuos frente a la variable dependiente Y. La Figura 2 muestra las diferentes posibilidades en un gráfico de residuos, mientras que el gráfico que se obtiene en el ejemplo manejado se refleja en la Figura 3.
Se puede complementar este análisis mediante gráficos de probabilidad normal y tests de normalidad para los residuos, como el de Kolmogorov-Smirnov (Figura 4). Así mismo, la independencia de las observaciones puede estudiarse mediante gráficos de autocorrelación y contrastes de independencia como el de Durbin-Watson.
Aunque obviaremos un análisis detallado de la verificación de las hipótesis del modelo, conviene hacer referencia a las medidas a tomar en caso de no cumplirse. Para el caso de no normalidad, resulta obvio que la medida más inmediata es la transformación de la variable dependiente, aunque otra alternativa son los cada vez más utilizados modelos de regresión no paramétrica, que evitan la suposición de una distribución gaussiana. También se debe modificar el modelo en el caso de datos dependientes o valores repetidos.
Predicción
Cuando se verifican las hipótesis sobre las que se asienta el modelo, la recta de regresión puede ser utilizada para predecir el valor medio de la variable Y para cada valor concreto de X. Calculando la esperanza matemática en ambos lados de la ecuación (1) se obtendrá:
![]()
de modo que la línea de regresión proporciona un estimador del valor medio de Y para cada valor de X. Como tal estimador, debemos considerar la incertidumbre asociada a esta recta, que puede ser reflejada mediante regiones de confianza que contienen a la recta. En la Figura 5 se muestra, superpuesta al diagrama de dispersión, la recta de regresión en el ejemplo de la tensión sistólica que estamos manejando, así como una región de confianza para la misma, que contendrá a la verdadera relación entre tensión sistólica y edad con una seguridad del 95%.
También se puede utilizar la recta de regresión como estimador del valor de Y en un individuo concreto. En este caso se esperará una mayor incertidumbre en la estimación que en el caso de predecir una tendencia media. En la Figura 4 se muestra además la banda de predicción para el ejemplo que estamos manejando, siendo ésta mucho más amplia que en el caso de intentar predecir el valor medio.
La regresión lineal simple es entonces una técnica sencilla y accesible para valorar la relación entre dos variables cuantitativas en la práctica clínica, proponiendo además un modelo al que se ajusta dicha relación. No debemos olvidar que a lo largo de este artículo hemos abordado el caso más sencillo en el que se obvia el problema de un número más elevado de variables entre las que valorar la relación. En este caso entraríamos de lleno en la temática de la regresión lineal múltiple, lo cual nos obligaría a abordar problemas de índole más complicado como el de la colinealidad, interacción entre variables, variables confusoras o un análisis más detallado de los residuos del modelo. Así mismo, no se debe pasar por alto el hecho de que en la mayoría de las aplicaciones prácticas la relación que se observa entre pares de variables no es tanto lineal como de tipo curvilíneo (ya sea una relación logarítmica, exponencial, polinómica, etc.). En estos casos, aunque se puede hablar de regresión curvilínea según el tipo de relación, una conveniente transformación de las variables reduce el problema al caso que acabamos de abordar.
Bibliografía
- Pita Fernández S, Rey Sierra T, Vila Alonso MT. Relaciones entre variables cuantitativas (I). Cadernos de Atención Primaria 1997; 4: 141-145.
- Seber GAF. Linear Regression Analysis. New York: John Wiley & Sons, 1977.
- Bland JM, Altman DG. Statistics Notes: Transforming data. BMJ 1996; 312:770. [Medline] [Texto completo]
- Härdle. Aplied Nonparametric Regression. Cambridge: University Press, 1990.
- Statistics notes: Correlation, regression and repeated data. BMJ 1994; 308: 896. [Texto completo]
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
- Etxebarría Murgiondo, J. Regresión Múltiple. Madrid: La Muralla; 1999.
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 2000; 7: 91-94






