Relación entre variables cuantitativas
Índice de contenidos
Introducción
En el análisis de los estudios clínico-epidemiológicos surge muy frecuentemente la necesidad de determinar la relación entre dos variables cuantitativas en un grupo de sujetos. Los objetivos de dicho análisis suelen ser:
- Determinar si las dos variables están correlacionadas, es decir si los valores de una variable tienden a ser más altos o más bajos para valores más altos o más bajos de la otra variable.
- Poder predecir el valor de una variable dado un valor determinado de la otra variable.
- Valorar el nivel de concordancia entre los valores de las dos variables.
Correlación
En este artículo trataremos de valorar la asociación entre dos variables cuantitativas estudiando el método conocido como correlación. Dicho cálculo es el primer paso para determinar la relación entre las variables. La predicción de una variable. La predicción de una variable dado un valor determinado de la otra precisa de la regresión lineal que abordaremos en otro artículo.
La cuantificación de la fuerza de la relación lineal entre dos variables cuantitativas, se estudia por medio del cálculo del coeficiente de correlación de Pearson. Dicho coeficiente oscila entre –1 y +1. Un valor de –1 indica una relación lineal o línea recta positiva perfecta. Una correlación próxima a cero indica que no hay relación lineal entre las dos variables.
El realizar la representación gráfica de los datos para demostrar la relación entre el valor del coeficiente de correlación y la forma de la gráfica es fundamental ya que existen relaciones no lineales.
El coeficiente de correlación posee las siguientes características:
- El valor del coeficiente de correlación es independiente de cualquier unidad usada para medir las variables.
- El valor del coeficiente de correlación se altera de forma importante ante la presencia de un valor extremo, como sucede con la desviación típica. Ante estas situaciones conviene realizar una transformación de datos que cambia la escala de medición y modera el efecto de valores extremos (como la transformación logarítmica).
- El coeficiente de correlación mide solo la relación con una línea recta. Dos variables pueden tener una relación curvilínea fuerte, a pesar de que su correlación sea pequeña. Por tanto cuando analicemos las relaciones entre dos variables debemos representarlas gráficamente y posteriormente calcular el coeficiente de correlación.
- El coeficiente de correlación no se debe extrapolar más allá del rango de valores observado de las variables a estudio ya que la relación existente entre X e Y puede cambiar fuera de dicho rango.
- La correlación no implica causalidad. La causalidad es un juicio de valor que requiere más información que un simple valor cuantitativo de un coeficiente de correlación.
El cálculo del coeficiente de correlación (r) entre peso y talla de 20 niños varones se muestra en la tabla 1. La covarianza, que en este ejemplo es el producto de peso (kg) por talla (cm), para que no tenga dimensión y sea un coeficiente, se divide por la desviación típica de X (talla) y por la desviación típica de Y (peso) con lo que obtenemos el coeficiente de correlación de Pearson que en este caso es de 0.885 e indica una importante correlación entre las dos variables. Es evidente que el hecho de que la correlación sea fuerte no implica causalidad. Si elevamos al cuadrado el coeficiente de correlación obtendremos el coeficiente de determinación (r2=0.783) que nos indica que el 78.3% de la variabilidad en el peso se explica por la talla del niño. Por lo tanto existen otras variables que modifican y explican la variabilidad del peso de estos niños. La introducción de más variable con técnicas de análisis multivariado nos permitirá identificar la importancia de que otras variables pueden tener sobre el peso.
| Tabla 1. Cálculo del Coeficiente de correlación de Pearson entre las variables talla y peso de 20 niños varones | ||||
|---|---|---|---|---|
|
Y Peso (Kg) |
X Talla (cm) |
|
|
|
|
9 |
72 |
5.65 |
1.4 |
7.91 |
|
|
||||
|
Sx = Desviación típica x = 8.087 Sy = Desviación típica y = 2.137 |
||||
Test de hipótesis de r
Tras realizar el cálculo del coeficiente de correlación de Pearson (r) debemos determinar si dicho coeficiente es estadísticamente diferente de cero. Para dicho calculo se aplica un test basado en la distribución de la t de student.
![]()
Si el valor del r calculado (en el ejemplo previo r = 0.885) supera al valor del error estándar multiplicado por la t de Student con n-2 grados de libertad, diremos que el coeficiente de correlación es significativo.
El nivel de significación viene dado por la decisión que adoptemos al buscar el valor en la tabla de la t de Student.
En el ejemplo previo con 20 niños, los grados de libertad son 18 y el valor de la tabla de la t de student para una seguridad del 95% es de 2.10 y para un 99% de seguridad el valor es 2.88. (Tabla 2).
![]()
Como quiera que r = 0.885 > a 2.10 * 0.109 = 2.30 podemos asegurar que el coeficiente de correlación es significativo (p<0.05). Si aplicamos el valor obtenido en la tabla de la t de Student para una seguridad del 99% (t = 2.88) observamos que como r = 0.885 sigue siendo > 2.88 * 0.109 = 0.313 podemos a su vez asegurar que el coeficiente es significativo (p<0.001). Este proceso de razonamiento es válido tanto para muestras pequeñas como para muestras grandes. En esta última situación podemos comprobar en la tabla de la t de student que para una seguridad del 95% el valor es 1.96 y para una seguridad del 99% el valor es 2.58.
Intervalo de confianza del coeficiente de correlación
La distribución del coeficiente de correlación de Pearson no es normal pero no se puede transformar r para conseguir un valor z que sigue una distribución normal (transformación de Fisher) y calcular a partir del valor z el intervalo de confianza.
La transformación es:
![]()
Ln representa el logaritmo neperiano en la base e
![]()
donde n representa el tamaño muestral. El 95% intervalo de confianza de z se calcula de la siguiente forma:
![]()
![]()
Tras calcular los intervalos de confianza con el valor z debemos volver a realizar el proceso inverso para calcular los intervalos del coeficiente r
![]()
Utilizando el ejemplo de la Tabla 1, obtenemos r = 0.885
![]()
95% intervalo de confianza de z
![]()
![]()
Tras calcular los intervalos de confianza de z debemos proceder a hacer el cálculo inverso para obtener los intervalos de confianza de coeficiente de correlación r que era lo que buscábamos en un principio antes de la transformación logarítmica.
![]()
0.726 a 0.953 son los intervalos de confianza (95%) de r.
Presentación de la correlación
Interpretación de la correlación
El coeficiente de correlación como previamente se indicó oscila entre –1 y +1 encontrándose en medio el valor 0 que indica que no existe asociación lineal entre las dos variables a estudio. Un coeficiente de valor reducido no indica necesariamente que no exista correlación ya que las variables pueden presentar una relación no lineal como puede ser el peso del recién nacido y el tiempo de gestación. En este caso el r infraestima la asociación al medirse linealmente. Los métodos no paramétrico estarían mejor utilizados en este caso para mostrar si las variables tienden a elevarse conjuntamente o a moverse en direcciones diferentes.
La significancia estadística de un coeficiente debe tenerse en cuenta conjuntamente con la relevancia clínica del fenómeno que estudiamos ya que coeficientes de 0.5 a 0.7 tienden ya a ser significativos como muestras pequeñas. Es por ello muy útil calcular el intervalo de confianza del r ya que en muestras pequeñas tenderá a ser amplio.
La estimación del coeficiente de determinación (r2) nos muestra el porcentaje de la variabilidad de los datos que se explica por la asociación entre las dos variables.
Como previamente se indicó la correlación elevada y estadísticamente significativa no tiene que asociarse a causalidad. Cuando objetivamos que dos variables están correlacionadas diversas razones pueden ser la causa de dicha correlación: a) pude que X influencie o cause Y, b) puede que influencie o cause X, c) X e Y pueden estar influenciadas por terceras variables que hace que se modifiquen ambas a la vez.
El coeficiente de correlación no debe utilizarse para comparar dos métodos que intentan medir el mismo evento, como por ejemplo dos instrumentos que miden la tensión arterial. El coeficiente de correlación mide el grado de asociación entre dos cantidades pero no mira el nivel de acuerdo o concordancia. Si los instrumentos de medida miden sistemáticamente cantidades diferentes uno del otro, la correlación puede ser 1 y su concordancia ser nula.
Coeficiente de correlación de los rangos de Spearman
Este coeficiente es una medida de asociación lineal que utiliza los rangos, números de orden, de cada grupo de sujetos y compara dichos rangos. Existen dos métodos para calcular el coeficiente de correlación de los rangos uno señalado por Spearman y otro por Kendall. El r de Spearman llamado también rho de Spearman es más fácil de calcular que el de Kendall. El coeficiente de correlación de Spearman es exactamente el mismo que el coeficiente de correlación de Pearson calculado sobre el rango de observaciones. En definitiva la correlación estimada entre X e Y se halla calculado el coeficiente de correlación de Pearson para el conjunto de rangos apareados. El coeficiente de correlación de Spearman es recomendable utilizarlo cuando los datos presentan valores externos ya que dichos valores afectan mucho el coeficiente de correlación de Pearson, o ante distribuciones no normales.
El cálculo del coeficiente viene dado por:
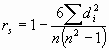
en donde di = rxi – ryi es la diferencia entre los rangos de X e Y.
Los valores de los rangos se colocan según el orden numérico de los datos de la variable.
Ejemplo: Se realiza un estudio para determinar la asociación entre la concentración de nicotina en sangre de un individuo y el contenido en nicotina de un cigarrillo (los valores de los rangos están entre paréntesis) .
|
X |
Y |
|---|---|
|
Concentración de Nicotina en sangre |
Contenido de Nicotina por cigarrillo |
|
185.7 (2) |
1.51 (8) |
|
197.3 (5) |
0.96 (3) |
|
204.2 (8) |
1.21 (6) |
|
199.9 (7) |
1.66 (10) |
|
199.1 (6) |
1.11 (4) |
|
192.8 (6) |
0.84 (2) |
|
207.4 (9) |
1.14 (5) |
|
183.0 (1) |
1.28 (7) |
|
234.1 (10) |
1.53 (9) |
|
196.5 (4) |
0.76 (1) |
Si existiesen valores coincidentes se pondría el promedio de los rangos que hubiesen sido asignado si no hubiese coincidencias. Por ejemplo si en una de las variables X tenemos:
|
X (edad) |
(Los rangos serían) |
|---|---|
|
23 |
1.5 |
| 23 | 1.5 |
| 27 | 3.5 |
| 27 | 3.5 |
| 39 | 5 |
| 41 | 6 |
| 45 | 7 |
| ... | ... |
Para el cálculo del ejemplo anterior de nicotina obtendríamos el siguiente resultado:
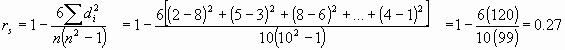
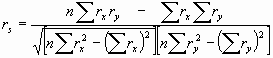
Si utilizamos la fórmula para calcular el coeficiente de correlación de Pearson de los rangos obtendríamos el mismo resultado
![]()
![]()
![]()
La interpretación del coeficiente rs de Spearman es similar a la Pearson. Valores próximos a 1 indican una correlación fuerte y positiva. Valores próximos a –1 indican una correlación fuerte y negativa. Valores próximos a cero indican que no hay correlación lineal. Así mismo el ![]() tiene el mismo significado que el coeficiente de determinación de r2.
tiene el mismo significado que el coeficiente de determinación de r2.
La distribución de rs es similar a la r por tanto el calculo de los intervalos de confianza de rs se pueden realizar utilizando la misma metodología previamente explicada para el coeficiente de correlación de Pearson.
| Tabla 2. Distribución t de Student |
|---|
|
.gif) |
Bibliografía
- Dawson-Saunders B, Trapp RG. Bioestadística Médica . 2ª ed. México: Editorial el Manual Moderno; 1996.
- Milton JS, Tsokos JO. Estadística para biología y ciencias de la salud. Madrid: Interamericana McGraw Hill; 2001.
- Martín Andrés A, Luna del Castillo JD. Bioestadística para las ciencias de la salud. 4ª ed. Madrid: ORMA; 1993.
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
- Pita Fernández S. Correlación frente a causalidad JANO 1996; (1174): 59-60.
- Feintein AR. Tempest in a P-pot?. (Editorial). Hypertension 1985; 7: 313-318. [Medline]
- Bland JM, Altman DG. Statistical methods for assesing agreement between two methods of clinical measurement. Lancet 1986; 1: 307-310. [Medline]
- Conover WJ. Practical nonparametric statistics. 3rd . ed. New York: John Wiley & Sons; 1998.
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
Cad Aten Primaria 1997; 4: 141-144.
Relación entre variables cuantitativas
Índice de contenidos
Introducción
En el análisis de los estudios clínico-epidemiológicos surge muy frecuentemente la necesidad de determinar la relación entre dos variables cuantitativas en un grupo de sujetos. Los objetivos de dicho análisis suelen ser:
- Determinar si las dos variables están correlacionadas, es decir si los valores de una variable tienden a ser más altos o más bajos para valores más altos o más bajos de la otra variable.
- Poder predecir el valor de una variable dado un valor determinado de la otra variable.
- Valorar el nivel de concordancia entre los valores de las dos variables.
Correlación
En este artículo trataremos de valorar la asociación entre dos variables cuantitativas estudiando el método conocido como correlación. Dicho cálculo es el primer paso para determinar la relación entre las variables. La predicción de una variable. La predicción de una variable dado un valor determinado de la otra precisa de la regresión lineal que abordaremos en otro artículo.
La cuantificación de la fuerza de la relación lineal entre dos variables cuantitativas, se estudia por medio del cálculo del coeficiente de correlación de Pearson. Dicho coeficiente oscila entre –1 y +1. Un valor de –1 indica una relación lineal o línea recta positiva perfecta. Una correlación próxima a cero indica que no hay relación lineal entre las dos variables.
El realizar la representación gráfica de los datos para demostrar la relación entre el valor del coeficiente de correlación y la forma de la gráfica es fundamental ya que existen relaciones no lineales.
El coeficiente de correlación posee las siguientes características:
- El valor del coeficiente de correlación es independiente de cualquier unidad usada para medir las variables.
- El valor del coeficiente de correlación se altera de forma importante ante la presencia de un valor extremo, como sucede con la desviación típica. Ante estas situaciones conviene realizar una transformación de datos que cambia la escala de medición y modera el efecto de valores extremos (como la transformación logarítmica).
- El coeficiente de correlación mide solo la relación con una línea recta. Dos variables pueden tener una relación curvilínea fuerte, a pesar de que su correlación sea pequeña. Por tanto cuando analicemos las relaciones entre dos variables debemos representarlas gráficamente y posteriormente calcular el coeficiente de correlación.
- El coeficiente de correlación no se debe extrapolar más allá del rango de valores observado de las variables a estudio ya que la relación existente entre X e Y puede cambiar fuera de dicho rango.
- La correlación no implica causalidad. La causalidad es un juicio de valor que requiere más información que un simple valor cuantitativo de un coeficiente de correlación.
El cálculo del coeficiente de correlación (r) entre peso y talla de 20 niños varones se muestra en la tabla 1. La covarianza, que en este ejemplo es el producto de peso (kg) por talla (cm), para que no tenga dimensión y sea un coeficiente, se divide por la desviación típica de X (talla) y por la desviación típica de Y (peso) con lo que obtenemos el coeficiente de correlación de Pearson que en este caso es de 0.885 e indica una importante correlación entre las dos variables. Es evidente que el hecho de que la correlación sea fuerte no implica causalidad. Si elevamos al cuadrado el coeficiente de correlación obtendremos el coeficiente de determinación (r2=0.783) que nos indica que el 78.3% de la variabilidad en el peso se explica por la talla del niño. Por lo tanto existen otras variables que modifican y explican la variabilidad del peso de estos niños. La introducción de más variable con técnicas de análisis multivariado nos permitirá identificar la importancia de que otras variables pueden tener sobre el peso.
| Tabla 1. Cálculo del Coeficiente de correlación de Pearson entre las variables talla y peso de 20 niños varones | ||||
|---|---|---|---|---|
|
Y Peso (Kg) |
X Talla (cm) |
|
|
|
|
9 |
72 |
5.65 |
1.4 |
7.91 |
|
|
||||
|
Sx = Desviación típica x = 8.087 Sy = Desviación típica y = 2.137 |
||||
Test de hipótesis de r
Tras realizar el cálculo del coeficiente de correlación de Pearson (r) debemos determinar si dicho coeficiente es estadísticamente diferente de cero. Para dicho calculo se aplica un test basado en la distribución de la t de student.
![]()
Si el valor del r calculado (en el ejemplo previo r = 0.885) supera al valor del error estándar multiplicado por la t de Student con n-2 grados de libertad, diremos que el coeficiente de correlación es significativo.
El nivel de significación viene dado por la decisión que adoptemos al buscar el valor en la tabla de la t de Student.
En el ejemplo previo con 20 niños, los grados de libertad son 18 y el valor de la tabla de la t de student para una seguridad del 95% es de 2.10 y para un 99% de seguridad el valor es 2.88. (Tabla 2).
![]()
Como quiera que r = 0.885 > a 2.10 * 0.109 = 2.30 podemos asegurar que el coeficiente de correlación es significativo (p<0.05). Si aplicamos el valor obtenido en la tabla de la t de Student para una seguridad del 99% (t = 2.88) observamos que como r = 0.885 sigue siendo > 2.88 * 0.109 = 0.313 podemos a su vez asegurar que el coeficiente es significativo (p<0.001). Este proceso de razonamiento es válido tanto para muestras pequeñas como para muestras grandes. En esta última situación podemos comprobar en la tabla de la t de student que para una seguridad del 95% el valor es 1.96 y para una seguridad del 99% el valor es 2.58.
Intervalo de confianza del coeficiente de correlación
La distribución del coeficiente de correlación de Pearson no es normal pero no se puede transformar r para conseguir un valor z que sigue una distribución normal (transformación de Fisher) y calcular a partir del valor z el intervalo de confianza.
La transformación es:
![]()
Ln representa el logaritmo neperiano en la base e
![]()
donde n representa el tamaño muestral. El 95% intervalo de confianza de z se calcula de la siguiente forma:
![]()
![]()
Tras calcular los intervalos de confianza con el valor z debemos volver a realizar el proceso inverso para calcular los intervalos del coeficiente r
![]()
Utilizando el ejemplo de la Tabla 1, obtenemos r = 0.885
![]()
95% intervalo de confianza de z
![]()
![]()
Tras calcular los intervalos de confianza de z debemos proceder a hacer el cálculo inverso para obtener los intervalos de confianza de coeficiente de correlación r que era lo que buscábamos en un principio antes de la transformación logarítmica.
![]()
0.726 a 0.953 son los intervalos de confianza (95%) de r.
Presentación de la correlación
Interpretación de la correlación
El coeficiente de correlación como previamente se indicó oscila entre –1 y +1 encontrándose en medio el valor 0 que indica que no existe asociación lineal entre las dos variables a estudio. Un coeficiente de valor reducido no indica necesariamente que no exista correlación ya que las variables pueden presentar una relación no lineal como puede ser el peso del recién nacido y el tiempo de gestación. En este caso el r infraestima la asociación al medirse linealmente. Los métodos no paramétrico estarían mejor utilizados en este caso para mostrar si las variables tienden a elevarse conjuntamente o a moverse en direcciones diferentes.
La significancia estadística de un coeficiente debe tenerse en cuenta conjuntamente con la relevancia clínica del fenómeno que estudiamos ya que coeficientes de 0.5 a 0.7 tienden ya a ser significativos como muestras pequeñas. Es por ello muy útil calcular el intervalo de confianza del r ya que en muestras pequeñas tenderá a ser amplio.
La estimación del coeficiente de determinación (r2) nos muestra el porcentaje de la variabilidad de los datos que se explica por la asociación entre las dos variables.
Como previamente se indicó la correlación elevada y estadísticamente significativa no tiene que asociarse a causalidad. Cuando objetivamos que dos variables están correlacionadas diversas razones pueden ser la causa de dicha correlación: a) pude que X influencie o cause Y, b) puede que influencie o cause X, c) X e Y pueden estar influenciadas por terceras variables que hace que se modifiquen ambas a la vez.
El coeficiente de correlación no debe utilizarse para comparar dos métodos que intentan medir el mismo evento, como por ejemplo dos instrumentos que miden la tensión arterial. El coeficiente de correlación mide el grado de asociación entre dos cantidades pero no mira el nivel de acuerdo o concordancia. Si los instrumentos de medida miden sistemáticamente cantidades diferentes uno del otro, la correlación puede ser 1 y su concordancia ser nula.
Coeficiente de correlación de los rangos de Spearman
Este coeficiente es una medida de asociación lineal que utiliza los rangos, números de orden, de cada grupo de sujetos y compara dichos rangos. Existen dos métodos para calcular el coeficiente de correlación de los rangos uno señalado por Spearman y otro por Kendall. El r de Spearman llamado también rho de Spearman es más fácil de calcular que el de Kendall. El coeficiente de correlación de Spearman es exactamente el mismo que el coeficiente de correlación de Pearson calculado sobre el rango de observaciones. En definitiva la correlación estimada entre X e Y se halla calculado el coeficiente de correlación de Pearson para el conjunto de rangos apareados. El coeficiente de correlación de Spearman es recomendable utilizarlo cuando los datos presentan valores externos ya que dichos valores afectan mucho el coeficiente de correlación de Pearson, o ante distribuciones no normales.
El cálculo del coeficiente viene dado por:
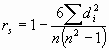
en donde di = rxi – ryi es la diferencia entre los rangos de X e Y.
Los valores de los rangos se colocan según el orden numérico de los datos de la variable.
Ejemplo: Se realiza un estudio para determinar la asociación entre la concentración de nicotina en sangre de un individuo y el contenido en nicotina de un cigarrillo (los valores de los rangos están entre paréntesis) .
|
X |
Y |
|---|---|
|
Concentración de Nicotina en sangre |
Contenido de Nicotina por cigarrillo |
|
185.7 (2) |
1.51 (8) |
|
197.3 (5) |
0.96 (3) |
|
204.2 (8) |
1.21 (6) |
|
199.9 (7) |
1.66 (10) |
|
199.1 (6) |
1.11 (4) |
|
192.8 (6) |
0.84 (2) |
|
207.4 (9) |
1.14 (5) |
|
183.0 (1) |
1.28 (7) |
|
234.1 (10) |
1.53 (9) |
|
196.5 (4) |
0.76 (1) |
Si existiesen valores coincidentes se pondría el promedio de los rangos que hubiesen sido asignado si no hubiese coincidencias. Por ejemplo si en una de las variables X tenemos:
|
X (edad) |
(Los rangos serían) |
|---|---|
|
23 |
1.5 |
| 23 | 1.5 |
| 27 | 3.5 |
| 27 | 3.5 |
| 39 | 5 |
| 41 | 6 |
| 45 | 7 |
| ... | ... |
Para el cálculo del ejemplo anterior de nicotina obtendríamos el siguiente resultado:
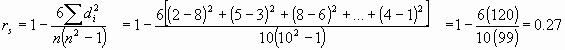
Si utilizamos la fórmula para calcular el coeficiente de correlación de Pearson de los rangos obtendríamos el mismo resultado

![]()
![]()
![]()
La interpretación del coeficiente rs de Spearman es similar a la Pearson. Valores próximos a 1 indican una correlación fuerte y positiva. Valores próximos a –1 indican una correlación fuerte y negativa. Valores próximos a cero indican que no hay correlación lineal. Así mismo el ![]() tiene el mismo significado que el coeficiente de determinación de r2.
tiene el mismo significado que el coeficiente de determinación de r2.
La distribución de rs es similar a la r por tanto el calculo de los intervalos de confianza de rs se pueden realizar utilizando la misma metodología previamente explicada para el coeficiente de correlación de Pearson.
| Tabla 2. Distribución t de Student |
|---|
|
.gif) |
Bibliografía
- Dawson-Saunders B, Trapp RG. Bioestadística Médica . 2ª ed. México: Editorial el Manual Moderno; 1996.
- Milton JS, Tsokos JO. Estadística para biología y ciencias de la salud. Madrid: Interamericana McGraw Hill; 2001.
- Martín Andrés A, Luna del Castillo JD. Bioestadística para las ciencias de la salud. 4ª ed. Madrid: ORMA; 1993.
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
- Pita Fernández S. Correlación frente a causalidad JANO 1996; (1174): 59-60.
- Feintein AR. Tempest in a P-pot?. (Editorial). Hypertension 1985; 7: 313-318. [Medline]
- Bland JM, Altman DG. Statistical methods for assesing agreement between two methods of clinical measurement. Lancet 1986; 1: 307-310. [Medline]
- Conover WJ. Practical nonparametric statistics. 3rd . ed. New York: John Wiley & Sons; 1998.
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
Cad Aten Primaria 1997; 4: 141-144.


