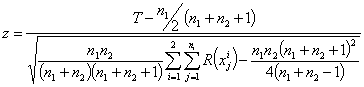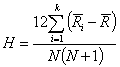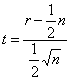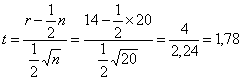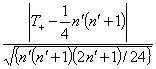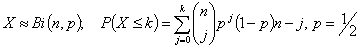Métodos no paramétricos para la comparación de dos muestras
Índice de contenidos
Introducción
A la hora de analizar los datos recogidos para una investigación, la elección de un método de análisis adecuado es crucial para evitar llegar a conclusiones erróneas. La selección de la técnica de análisis más apropiada ha de hacerse tomando en cuenta distintos aspectos relativos al diseño del estudio y a la naturaleza de los datos que se quieren cuantificar. El número de grupos de observaciones a comparar, la naturaleza de las mimas (según se trate de muestras independientes u observaciones repetidas sobre los mismos individuos), el tipo de datos (variables continuas / cualitativas) o su distribución de probabilidad son elementos determinantes a la hora de conocer las técnicas estadísticas que se pueden utilizar.
En el análisis de datos cuantitativos, los métodos estadísticos más conocidos y utilizados en la práctica, como el test t de Student o el análisis de la varianza, se basan en asunciones que no siempre son verificadas por los datos de los que se dispone. Así, es frecuente tener que asumir que la variable objeto de interés sigue por ejemplo una distribución gaussiana. Cuando la ausencia de normalidad es obvia, o no puede ser totalmente asumida por un tamaño muestral reducido, suele recurrirse a una transformación de la variable de interés (por ejemplo, la transformación logarítmica) para simetrizar su distribución o bien justificar el uso de las técnicas habituales recurriendo a su robustez (esto es, su escasa sensibilidad a la ausencia de normalidad). Existen a su vez otros métodos, usualmente llamados no paramétricos, que no requieren de este tipo de hipótesis sobre la distribución de los datos, resultan fáciles de implementar y pueden calcularse incluso con tamaños de muestra reducidos. En el presente trabajo se describirán algunos de los métodos no paramétricos más utilizados en la práctica.
Dos muestras independientes: la prueba U de Mann-Whitney y la prueba de la suma de rangos de Wilcoxon
En muchas situaciones se desea contrastar si la distribución de una variable X es igual en dos poblaciones, o bien si dicha variable tiende a ser mayor (o menor) en alguno de los dos grupos, basándose en los datos muestrales. Por ejemplo, puede resultar interesante comparar el descenso de peso en pacientes sometidos a dos dietas alimenticias distintas, o el nivel de dolor en sujetos con artrosis que reciben un tratamiento frente a placebo. En la teoría estadística “tradicional” la prueba que se aplicaría para realizar este tipo de comparaciones sería el test t de Student para dos muestras independientes, siendo la U de Mann-Whitney o la prueba de la suma de rangos de Wilcoxon pruebas de carácter no paramétrico equivalentes que podrían emplearse también en esta situación.
De un modo más formal, supongamos que se dispone de observaciones de una misma variable X (pérdida de peso, puntuación de dolor, etc.) en dos poblaciones distintas sobre muestras de tamaño n1 y n2, respectivamente:
| Población 1: |
|
|
| Población 2: |
|
Un modo intuitivo de proceder consiste en ordenar las observaciones obtenidas, independientemente de su población de origen, de menor a mayor valor y asignar rangos a los datos así ordenados. De esta forma, a la observación con un valor más pequeño se le asigna rango 1, a la siguiente rango 2, y así sucesivamente. En caso de empates (si dos o más observaciones coinciden en valor) se le asignará a cada una de estas observaciones el promedio de los rangos que les serían asignados si no hubiese empate.
Si no existiesen diferencias en la distribución entre ambas poblaciones, los rangos deberían mezclarse aleatoriamente entre las dos muestras. En cambio, si la suma de los rangos asignados a las observaciones de una de las poblaciones resulta mucho mayor que la suma de los rangos asignados a las observaciones de la otra población, esto indicaría una diferencia en la distribución de la variable X entre ambas.
Denotemos por ![]() el rango asignado a cada una de las observaciones disponibles. Consideraremos como estadístico de contraste para la prueba de la suma de rangos de Wilcoxon la suma de los rangos en una de las poblaciones:
el rango asignado a cada una de las observaciones disponibles. Consideraremos como estadístico de contraste para la prueba de la suma de rangos de Wilcoxon la suma de los rangos en una de las poblaciones:
|
La distribución de probabilidad de los estadísticos anteriores ha sido tabulada para tamaños de muestra pequeños y en el caso de no existir empates (Tabla 1). Así, la Tabla 1 sirve para conocer si el resultado es significativo a nivel bilateral si se trabaja con una seguridad del 95% y tamaños muestrales ≤15.
Para tamaños muestrales mayores (>15), es adecuado utilizar la aproximación normal, obteniendo a partir de T la variable:
|
donde ![]() y
y ![]() son la media y desviación estándar de T si la hipótesis nula es cierta, y vienen dadas por las siguientes fórmulas:
son la media y desviación estándar de T si la hipótesis nula es cierta, y vienen dadas por las siguientes fórmulas:
|
El número de empates debe ser además pequeño en relación con el número total de observaciones. En el caso de empates, la varianza del estadístico T debe modificarse, de modo que la expresión anterior quedaría como sigue:
|
Una vez obtenido el valor de z éste se debe referir a las tablas de la distribución normal para obtener el valor de significación asociado.
Para ilustrar el uso de esta prueba, consideraremos los datos de la Tabla 2, correspondiente a los valores de medición del dolor (en una escala de 0 a 10) en dos grupos de 11 pacientes sometidos a dos tratamientos analgésicos diferentes. En este caso n1=n2=11. La suma de los rangos asignados a las observaciones del primer grupo es T=171, y su media
|
Puesto que la suma de rangos obtenida supera a la esperada, consideraremos como estadístico final T=171-126,5=44,5, y lo referiremos a los valores en la Tabla 1. Trabajando con un planteamiento bilateral y una seguridad del 95%, la región de rechazo corresponde a valores de T menores o iguales a 96, por lo cual se rechazaría la hipótesis nula de igual nivel de dolor en ambos grupos de tratamiento con un nivel de significación p<0.05.
En el ejemplo propuesto podemos comprobar el resultado que se obtendría al utilizar la aproximación normal. Tal y como vimos:
|
|
Con lo cual se utilizaría el estadístico:
|
que debe referirse a los valores de una distribución normal estándar. Así, se obtiene p=0,002, concluyéndose igualmente que el nivel de dolor es diferente según la terapia analgésica utilizada.
Por otra parte, es frecuente referirse a la prueba de la suma de rangos de Wilcoxon con el nombre de prueba U de Mann-Whitney. En realidad, son dos pruebas diferentes, aunque esencialmente equivalentes entre sí. Para el cálculo de la prueba U de Mann-Whitney, en lugar de la suma de rangos se calcularán los valores:
U12: el número de pares para los cuales una observación de la primera población es inferior a una observación de la segunda población,![]() .
.
U21: el número de pares para los cuales una observación de la primera población es superior a una observación de la segunda población,![]() .
.
En caso de empate se contabilizarán 0,5 unidades a mayores en cada una de las cantidades anteriores. De forma análoga a como ocurría con la prueba anterior, valores bajos de U12 indicarán una diferencia hacia valores más altos de la variable en la primera población, mientras que valores altos indicarán que estos tienden a ser más altos en la segunda población.
Los parámetros anteriores se relacionan con el estadístico T descrito anteriormente mediante la siguiente ecuación:
|
De forma que a partir del estadístico U puede obtenerse inmediatamente el valor del estadístico de Wilcoxon y utilizar la metodología anterior para obtener el valor de significación asociado. De hecho, la mayor parte de programas estadísticos, como el SPSS, muestran en sus salidas los valores de ambos estadísticos, junto con un p-valor común, bien calculado a partir de la aproximación asintótica mediante una distribución normal o a partir de las tabulaciones correspondientes, corrigiendo la posibilidad de empates. Otra prueba equivalente aunque menos conocida es la S de Kendall, calculada según S= U12- U21.
Por último, decir que al igual que el análisis de la varianza en el abordaje estadístico “tradicional” extiende la prueba t de Student al caso en el que se quieran comparar más de dos grupos, el test de Kruskall-Wallis es una extensión natural de la prueba de Mann-Whitney a esta situación. Para su cálculo se ordenarán las N observaciones obtenidas, independientemente de su población de origen, de menor a mayor valor y se asignarán los rangos correspondientes. El estadístico de contraste para la prueba de Kruskall-Wallis vendrá dado por:
|
donde N denota al número total de observaciones en los k grupos que se comparan, ![]() es el promedio de los rangos de las observaciones del i-ésimo grupo y
es el promedio de los rangos de las observaciones del i-ésimo grupo y ![]() el promedio de todos los rangos. Así definido, el estadístico H sigue una distribución
el promedio de todos los rangos. Así definido, el estadístico H sigue una distribución ![]() con k-1 grados de libertad.
con k-1 grados de libertad.
Dos muestras relacionadas: la prueba del signo y la prueba de la suma de rangos con signo de Wilcoxon
Otra situación muy frecuente es aquella en la que se desea comparar la distribución de una variable X en dos muestras de casos apareados, usualmente sobre los mismos individuos en dos momentos diferentes de tiempo. Por ejemplo, puede quererse comparar el nivel de dolor en una articulación antes y después de un tratamiento con infiltraciones, o el peso antes y después de someterse a algún programa de adelgazamiento. En estas situaciones, es lógico trabajar con la diferencia de las observaciones entre ambos momentos (pérdida de peso, disminución del nivel de dolor, etc.):
|
donde aquí ![]() denotan los valores observados de la variable X en n individuos en el primer instante y
denotan los valores observados de la variable X en n individuos en el primer instante y ![]() los valores observados en un instante posterior.
los valores observados en un instante posterior.
Una forma sencilla de proceder consiste en contabilizar el número r de diferencias positivas y el número s de diferencias negativas (sin contar los valores 0). Bajo la hipótesis nula de que no existen diferencias, será igualmente probable obtener una diferencia positiva o negativa, por lo que ambos valores se distribuirán según una distribución binomial de parámetros Bi(r+s,1/2). Recurriendo a las tablas de la distribución binomial, podemos obtener a partir de r (o, equivalentemente, de s) el valor exacto de significación asociado (Tabla 3).
Como ejemplo, utilizaremos los datos de la Tabla 4 en la que se muestra la pérdida de peso alcanzada por 20 sujetos sometidos a un programa de adelgazamiento. El número de observaciones positivas (pacientes que realmente perdieron peso) es r=14, mientras que el número de observaciones negativas (pacientes que ganaron peso) es s=6. Refiriendo estos valores a los de una distribución binomial de parámetros Bi(20,1/2) se obtiene un valor de p=2x0,058=0,116, por lo que no puede concluirse que exista una pérdida de peso significativa en los pacientes estudiados.
Para tamaños muestrales grandes (n≥20) puede utilizarse como estadístico de contraste:
|
que seguirá aproximadamente una distribución normal estándar N(0,1).
En el ejemplo anterior:
|
Si referimos el valor obtenido a la función de probabilidad de una distribución N(0,1) se obtiene p=0.075, no resultando en un valor significativo tal y como ocurría con la aproximación por la binomial.
La prueba del signo, tal y como se denomina a la prueba que se acaba de describir, presenta como mayor limitación el hecho de que no tiene en cuenta la magnitud (positiva o negativa) de las observaciones. Así, puede ocurrir que existan muchas diferencias positivas pero de escasa magnitud (pacientes que pierden peso pero en poco volumen) y pocas diferencias negativas pero de mucha mayor importancia (pacientes que ganan mucho peso). Este tipo de situaciones deberían reducir la posibilidad de encontrar diferencias significativas entre las observaciones.
La prueba de la suma de rangos con signo de Wilcoxon toma en consideración la deficiencia anterior. Las observaciones se ordenan de menor a mayor valor absoluto y se les asignan rangos (ignorando los valores nulos y actuando igual que en el caso de la prueba de suma de rangos ante empates). Se utilizará como estadístico de contraste la suma T+ de los rangos asignados a valores positivos o bien la suma T- de los rangos asignados a valores negativos. Para valores pequeños de n, la distribución de T+ y T- está completamente tabulada, y puede utilizarse para obtener los valores críticos del test (Tabla 5). En el caso de muestras grandes (n≥20), la distribución de T+ y T- puede aproximarse por la de una variable normal. Así, realizando la transformación:
|
la distribución asociada es la de una normal estándar (donde n’ es el número de observaciones no nulas).
Al igual que ocurría en la prueba de la suma de rangos para muestras independientes, en caso de empate la varianza del estadístico varía y debería efectuarse alguna corrección en la expresión anterior. Así mismo, los valores críticos en la Tabla 5 para el caso de empates suelen resultar algo conservadores, es decir, con empates se tenderá a aceptar la hipótesis nula de no diferencias cuando en realidad ésta debería ser rechazada.
Volviendo al ejemplo anterior, y tras ordenar las observaciones en la Tabla 4 de menor a mayor valor absoluto, se obtiene las sumas de rangos T+=178,5 y T-=31,5 correspondientes a las observaciones con pérdida o ganancia de peso, respectivamente. Refiriendo estos valores a los que se muestran en la Tabla 5 con n=20, se obtiene un valor de p<0.01.
Obviamente, el tipo de procedimientos aquí expuestos permiten cubrir sólo una pequeña parte de las situaciones que se nos pueden plantear en la práctica. En la mayoría de las ocasiones, se dispone de información en una gran cantidad de variables, lo cual requiere recurrir a otros métodos de análisis que no sólo permitan estudiar las relaciones entre un par de variables, sino estudiar el efecto conjunto de todas ellas.
Anexo
| Tabla 2. Valores de medición del dolor (en una escala de 0 a 10) en dos grupos de pacientes sometidos a dos tratamientos analgésicos diferentes. | ||||
|---|---|---|---|---|
|
|
Tratamiento A | Rango asignado | Tratamiento B | Rango asignado |
| 1 | 100 | 22 | 85 | 18 |
| 2 | 85 | 18 | 62 | 8 |
| 3 | 72 | 15 | 57 | 6.5 |
| 4 | 64 | 9.5 | 32 | 1 |
| 5 | 70 | 12.5 | 70 | 12.5 |
| 6 | 56 | 5 | 54 | 4 |
| 7 | 87 | 20 | 45 | 2 |
| 8 | 71 | 14 | 50 | 3 |
| 9 | 95 | 21 | 64 | 9.5 |
| 10 | 80 | 16 | 66 | 11 |
| 11 | 85 | 18 | 57 | 6.5 |
| Suma de rangos | 171 | 82 | ||
Bibliografía
- Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991. [Índice]
- Armitage P, Berry G. Estadística para la investigación biomédica. 3ª ed. Barcelona: Doyma; 1997.
- Milton JS., Tsokos JO. Estadística para biología y ciencias de la salud. 3ª ed. Madrid: Interamericana McGraw Hill; 2007.
- Pértega Díaz S, Pita Fernández S. Métodos paramétricos para la comparación de dos medias. T de Student. Cad Aten Primaria 2001; 8. 37-41. [Texto completo]
- Pértega Díaz S, Pita Fernández S. La distribución normal. Cad Aten Primaria 2001; 8: 268-274. [Texto completo]
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España).
Centro de Salud de Cambre (A Coruña).
Métodos no paramétricos para la comparación de dos muestras
Índice de contenidos
Introducción
A la hora de analizar los datos recogidos para una investigación, la elección de un método de análisis adecuado es crucial para evitar llegar a conclusiones erróneas. La selección de la técnica de análisis más apropiada ha de hacerse tomando en cuenta distintos aspectos relativos al diseño del estudio y a la naturaleza de los datos que se quieren cuantificar. El número de grupos de observaciones a comparar, la naturaleza de las mimas (según se trate de muestras independientes u observaciones repetidas sobre los mismos individuos), el tipo de datos (variables continuas / cualitativas) o su distribución de probabilidad son elementos determinantes a la hora de conocer las técnicas estadísticas que se pueden utilizar.
En el análisis de datos cuantitativos, los métodos estadísticos más conocidos y utilizados en la práctica, como el test t de Student o el análisis de la varianza, se basan en asunciones que no siempre son verificadas por los datos de los que se dispone. Así, es frecuente tener que asumir que la variable objeto de interés sigue por ejemplo una distribución gaussiana. Cuando la ausencia de normalidad es obvia, o no puede ser totalmente asumida por un tamaño muestral reducido, suele recurrirse a una transformación de la variable de interés (por ejemplo, la transformación logarítmica) para simetrizar su distribución o bien justificar el uso de las técnicas habituales recurriendo a su robustez (esto es, su escasa sensibilidad a la ausencia de normalidad). Existen a su vez otros métodos, usualmente llamados no paramétricos, que no requieren de este tipo de hipótesis sobre la distribución de los datos, resultan fáciles de implementar y pueden calcularse incluso con tamaños de muestra reducidos. En el presente trabajo se describirán algunos de los métodos no paramétricos más utilizados en la práctica.
Dos muestras independientes: la prueba U de Mann-Whitney y la prueba de la suma de rangos de Wilcoxon
En muchas situaciones se desea contrastar si la distribución de una variable X es igual en dos poblaciones, o bien si dicha variable tiende a ser mayor (o menor) en alguno de los dos grupos, basándose en los datos muestrales. Por ejemplo, puede resultar interesante comparar el descenso de peso en pacientes sometidos a dos dietas alimenticias distintas, o el nivel de dolor en sujetos con artrosis que reciben un tratamiento frente a placebo. En la teoría estadística “tradicional” la prueba que se aplicaría para realizar este tipo de comparaciones sería el test t de Student para dos muestras independientes, siendo la U de Mann-Whitney o la prueba de la suma de rangos de Wilcoxon pruebas de carácter no paramétrico equivalentes que podrían emplearse también en esta situación.
De un modo más formal, supongamos que se dispone de observaciones de una misma variable X (pérdida de peso, puntuación de dolor, etc.) en dos poblaciones distintas sobre muestras de tamaño n1 y n2, respectivamente:
| Población 1: |
|
|
| Población 2: |
|
Un modo intuitivo de proceder consiste en ordenar las observaciones obtenidas, independientemente de su población de origen, de menor a mayor valor y asignar rangos a los datos así ordenados. De esta forma, a la observación con un valor más pequeño se le asigna rango 1, a la siguiente rango 2, y así sucesivamente. En caso de empates (si dos o más observaciones coinciden en valor) se le asignará a cada una de estas observaciones el promedio de los rangos que les serían asignados si no hubiese empate.
Si no existiesen diferencias en la distribución entre ambas poblaciones, los rangos deberían mezclarse aleatoriamente entre las dos muestras. En cambio, si la suma de los rangos asignados a las observaciones de una de las poblaciones resulta mucho mayor que la suma de los rangos asignados a las observaciones de la otra población, esto indicaría una diferencia en la distribución de la variable X entre ambas.
Denotemos por ![]() el rango asignado a cada una de las observaciones disponibles. Consideraremos como estadístico de contraste para la prueba de la suma de rangos de Wilcoxon la suma de los rangos en una de las poblaciones:
el rango asignado a cada una de las observaciones disponibles. Consideraremos como estadístico de contraste para la prueba de la suma de rangos de Wilcoxon la suma de los rangos en una de las poblaciones:
|
La distribución de probabilidad de los estadísticos anteriores ha sido tabulada para tamaños de muestra pequeños y en el caso de no existir empates (Tabla 1). Así, la Tabla 1 sirve para conocer si el resultado es significativo a nivel bilateral si se trabaja con una seguridad del 95% y tamaños muestrales ≤15.
Para tamaños muestrales mayores (>15), es adecuado utilizar la aproximación normal, obteniendo a partir de T la variable:
|
donde ![]() y
y ![]() son la media y desviación estándar de T si la hipótesis nula es cierta, y vienen dadas por las siguientes fórmulas:
son la media y desviación estándar de T si la hipótesis nula es cierta, y vienen dadas por las siguientes fórmulas:
|
El número de empates debe ser además pequeño en relación con el número total de observaciones. En el caso de empates, la varianza del estadístico T debe modificarse, de modo que la expresión anterior quedaría como sigue:
|
Una vez obtenido el valor de z éste se debe referir a las tablas de la distribución normal para obtener el valor de significación asociado.
Para ilustrar el uso de esta prueba, consideraremos los datos de la Tabla 2, correspondiente a los valores de medición del dolor (en una escala de 0 a 10) en dos grupos de 11 pacientes sometidos a dos tratamientos analgésicos diferentes. En este caso n1=n2=11. La suma de los rangos asignados a las observaciones del primer grupo es T=171, y su media
|
Puesto que la suma de rangos obtenida supera a la esperada, consideraremos como estadístico final T=171-126,5=44,5, y lo referiremos a los valores en la Tabla 1. Trabajando con un planteamiento bilateral y una seguridad del 95%, la región de rechazo corresponde a valores de T menores o iguales a 96, por lo cual se rechazaría la hipótesis nula de igual nivel de dolor en ambos grupos de tratamiento con un nivel de significación p<0.05.
En el ejemplo propuesto podemos comprobar el resultado que se obtendría al utilizar la aproximación normal. Tal y como vimos:
|
|
Con lo cual se utilizaría el estadístico:
|
que debe referirse a los valores de una distribución normal estándar. Así, se obtiene p=0,002, concluyéndose igualmente que el nivel de dolor es diferente según la terapia analgésica utilizada.
Por otra parte, es frecuente referirse a la prueba de la suma de rangos de Wilcoxon con el nombre de prueba U de Mann-Whitney. En realidad, son dos pruebas diferentes, aunque esencialmente equivalentes entre sí. Para el cálculo de la prueba U de Mann-Whitney, en lugar de la suma de rangos se calcularán los valores:
U12: el número de pares para los cuales una observación de la primera población es inferior a una observación de la segunda población,![]() .
.
U21: el número de pares para los cuales una observación de la primera población es superior a una observación de la segunda población,![]() .
.
En caso de empate se contabilizarán 0,5 unidades a mayores en cada una de las cantidades anteriores. De forma análoga a como ocurría con la prueba anterior, valores bajos de U12 indicarán una diferencia hacia valores más altos de la variable en la primera población, mientras que valores altos indicarán que estos tienden a ser más altos en la segunda población.
Los parámetros anteriores se relacionan con el estadístico T descrito anteriormente mediante la siguiente ecuación:
|
De forma que a partir del estadístico U puede obtenerse inmediatamente el valor del estadístico de Wilcoxon y utilizar la metodología anterior para obtener el valor de significación asociado. De hecho, la mayor parte de programas estadísticos, como el SPSS, muestran en sus salidas los valores de ambos estadísticos, junto con un p-valor común, bien calculado a partir de la aproximación asintótica mediante una distribución normal o a partir de las tabulaciones correspondientes, corrigiendo la posibilidad de empates. Otra prueba equivalente aunque menos conocida es la S de Kendall, calculada según S= U12- U21.
Por último, decir que al igual que el análisis de la varianza en el abordaje estadístico “tradicional” extiende la prueba t de Student al caso en el que se quieran comparar más de dos grupos, el test de Kruskall-Wallis es una extensión natural de la prueba de Mann-Whitney a esta situación. Para su cálculo se ordenarán las N observaciones obtenidas, independientemente de su población de origen, de menor a mayor valor y se asignarán los rangos correspondientes. El estadístico de contraste para la prueba de Kruskall-Wallis vendrá dado por:
|
donde N denota al número total de observaciones en los k grupos que se comparan, ![]() es el promedio de los rangos de las observaciones del i-ésimo grupo y
es el promedio de los rangos de las observaciones del i-ésimo grupo y ![]() el promedio de todos los rangos. Así definido, el estadístico H sigue una distribución
el promedio de todos los rangos. Así definido, el estadístico H sigue una distribución ![]() con k-1 grados de libertad.
con k-1 grados de libertad.
Dos muestras relacionadas: la prueba del signo y la prueba de la suma de rangos con signo de Wilcoxon
Otra situación muy frecuente es aquella en la que se desea comparar la distribución de una variable X en dos muestras de casos apareados, usualmente sobre los mismos individuos en dos momentos diferentes de tiempo. Por ejemplo, puede quererse comparar el nivel de dolor en una articulación antes y después de un tratamiento con infiltraciones, o el peso antes y después de someterse a algún programa de adelgazamiento. En estas situaciones, es lógico trabajar con la diferencia de las observaciones entre ambos momentos (pérdida de peso, disminución del nivel de dolor, etc.):
|
donde aquí ![]() denotan los valores observados de la variable X en n individuos en el primer instante y
denotan los valores observados de la variable X en n individuos en el primer instante y ![]() los valores observados en un instante posterior.
los valores observados en un instante posterior.
Una forma sencilla de proceder consiste en contabilizar el número r de diferencias positivas y el número s de diferencias negativas (sin contar los valores 0). Bajo la hipótesis nula de que no existen diferencias, será igualmente probable obtener una diferencia positiva o negativa, por lo que ambos valores se distribuirán según una distribución binomial de parámetros Bi(r+s,1/2). Recurriendo a las tablas de la distribución binomial, podemos obtener a partir de r (o, equivalentemente, de s) el valor exacto de significación asociado (Tabla 3).
Como ejemplo, utilizaremos los datos de la Tabla 4 en la que se muestra la pérdida de peso alcanzada por 20 sujetos sometidos a un programa de adelgazamiento. El número de observaciones positivas (pacientes que realmente perdieron peso) es r=14, mientras que el número de observaciones negativas (pacientes que ganaron peso) es s=6. Refiriendo estos valores a los de una distribución binomial de parámetros Bi(20,1/2) se obtiene un valor de p=2x0,058=0,116, por lo que no puede concluirse que exista una pérdida de peso significativa en los pacientes estudiados.
Para tamaños muestrales grandes (n≥20) puede utilizarse como estadístico de contraste:
|
que seguirá aproximadamente una distribución normal estándar N(0,1).
En el ejemplo anterior:
|
Si referimos el valor obtenido a la función de probabilidad de una distribución N(0,1) se obtiene p=0.075, no resultando en un valor significativo tal y como ocurría con la aproximación por la binomial.
La prueba del signo, tal y como se denomina a la prueba que se acaba de describir, presenta como mayor limitación el hecho de que no tiene en cuenta la magnitud (positiva o negativa) de las observaciones. Así, puede ocurrir que existan muchas diferencias positivas pero de escasa magnitud (pacientes que pierden peso pero en poco volumen) y pocas diferencias negativas pero de mucha mayor importancia (pacientes que ganan mucho peso). Este tipo de situaciones deberían reducir la posibilidad de encontrar diferencias significativas entre las observaciones.
La prueba de la suma de rangos con signo de Wilcoxon toma en consideración la deficiencia anterior. Las observaciones se ordenan de menor a mayor valor absoluto y se les asignan rangos (ignorando los valores nulos y actuando igual que en el caso de la prueba de suma de rangos ante empates). Se utilizará como estadístico de contraste la suma T+ de los rangos asignados a valores positivos o bien la suma T- de los rangos asignados a valores negativos. Para valores pequeños de n, la distribución de T+ y T- está completamente tabulada, y puede utilizarse para obtener los valores críticos del test (Tabla 5). En el caso de muestras grandes (n≥20), la distribución de T+ y T- puede aproximarse por la de una variable normal. Así, realizando la transformación:
|
la distribución asociada es la de una normal estándar (donde n’ es el número de observaciones no nulas).
Al igual que ocurría en la prueba de la suma de rangos para muestras independientes, en caso de empate la varianza del estadístico varía y debería efectuarse alguna corrección en la expresión anterior. Así mismo, los valores críticos en la Tabla 5 para el caso de empates suelen resultar algo conservadores, es decir, con empates se tenderá a aceptar la hipótesis nula de no diferencias cuando en realidad ésta debería ser rechazada.
Volviendo al ejemplo anterior, y tras ordenar las observaciones en la Tabla 4 de menor a mayor valor absoluto, se obtiene las sumas de rangos T+=178,5 y T-=31,5 correspondientes a las observaciones con pérdida o ganancia de peso, respectivamente. Refiriendo estos valores a los que se muestran en la Tabla 5 con n=20, se obtiene un valor de p<0.01.
Obviamente, el tipo de procedimientos aquí expuestos permiten cubrir sólo una pequeña parte de las situaciones que se nos pueden plantear en la práctica. En la mayoría de las ocasiones, se dispone de información en una gran cantidad de variables, lo cual requiere recurrir a otros métodos de análisis que no sólo permitan estudiar las relaciones entre un par de variables, sino estudiar el efecto conjunto de todas ellas.
Anexo
| Tabla 2. Valores de medición del dolor (en una escala de 0 a 10) en dos grupos de pacientes sometidos a dos tratamientos analgésicos diferentes. | ||||
|---|---|---|---|---|
|
|
Tratamiento A | Rango asignado | Tratamiento B | Rango asignado |
| 1 | 100 | 22 | 85 | 18 |
| 2 | 85 | 18 | 62 | 8 |
| 3 | 72 | 15 | 57 | 6.5 |
| 4 | 64 | 9.5 | 32 | 1 |
| 5 | 70 | 12.5 | 70 | 12.5 |
| 6 | 56 | 5 | 54 | 4 |
| 7 | 87 | 20 | 45 | 2 |
| 8 | 71 | 14 | 50 | 3 |
| 9 | 95 | 21 | 64 | 9.5 |
| 10 | 80 | 16 | 66 | 11 |
| 11 | 85 | 18 | 57 | 6.5 |
| Suma de rangos | 171 | 82 | ||
Bibliografía
- Altman DG. Practical Statistics for Medical Research. London: Chapman & Hall, 1991. [Índice]
- Armitage P, Berry G. Estadística para la investigación biomédica. 3ª ed. Barcelona: Doyma; 1997.
- Milton JS., Tsokos JO. Estadística para biología y ciencias de la salud. 3ª ed. Madrid: Interamericana McGraw Hill; 2007.
- Pértega Díaz S, Pita Fernández S. Métodos paramétricos para la comparación de dos medias. T de Student. Cad Aten Primaria 2001; 8. 37-41. [Texto completo]
- Pértega Díaz S, Pita Fernández S. La distribución normal. Cad Aten Primaria 2001; 8: 268-274. [Texto completo]
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España).
Centro de Salud de Cambre (A Coruña).