Medidas de concordancia: el índice Kappa
Índice de contenidos
Introducción
En cualquier estudio de investigación una cuestión clave es la fiabilidad de los procedimientos de medida empleados. Como señala Fleiss en el contexto de los estudios clínicos, ni el más elegante de los diseños sería capaz de paliar el daño causado por un sistema de medida poco fiable.
Tradicionalmente se ha reconocido una fuente importante de error de medida en la variabilidad entre observadores . Consecuentemente, un objetivo de los estudios de fiabilidad debe consistir en estimar el grado de dicha variabilidad.
En este sentido, dos aspectos distintos entran a formar parte típicamente del estudio de fiabilidad: de una parte, el sesgo entre observadores –dicho con menos rigor, la tendencia de un observador a dar consistentemente valores mayores que otro– y de otra, la concordancia entre observadores –es decir, hasta qué punto los observadores coinciden en su medición–.
Ciñéndonos a este segundo aspecto, la manera concreta de abordar el problema depende estrechamente de la naturaleza de los datos: si éstos son de tipo continuo es habitual la utilización de estimadores del coeficiente de correlación intraclase, mientras que cuando se trata de datos de tipo categórico el estadístico más empleado es el índice kappa, al que dedicamos el resto de este artículo.
El índice Kappa
Supongamos que dos observadores distintos clasifican independientemente una muestra de n ítems en un mismo conjunto de C categorías nominales. El resultado de esta clasificación se puede resumir en una tabla como la tabla 1, en la que cada valor xij representa el número de ítems que han sido clasificados por el observador 1 en la categoría i y por el observador 2 en la categoría j.
| Tabla 1. Formato de los datos en un estudio de concordancia | |||||
|---|---|---|---|---|---|
|
Observador 2
|
|||||
|
Observador 1
|
1 |
2 |
… |
C |
Total
|
|
1
|
X11 |
X12 |
… |
X1C |
X1 |
|
2
|
X21 |
X22 |
… |
X2C |
X2 |
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
C
|
XC1 |
XC2 |
… |
XCC |
XC |
|
Total
|
X.1 |
X.2 |
… |
X.C |
n |
Por ejemplo, podemos pensar en dos radiólogos enfrentados a la tarea de categorizar una muestra de radiografías mediante la escala: "anormal, "dudosa", "normal". La tabla 2 muestra un conjunto de datos hipotéticos para este ejemplo, dispuesto de acuerdo con el esquema de la tabla 1.
| Tabla 2. Datos hipotéticos de clasificación de una muestra de 100 radiografías por dos radiólogos | ||||
|---|---|---|---|---|
|
Radiólogo 2
|
||||
|
Radiólogo 1
|
Anormal |
Dudosa |
Normal |
Total |
|
Anormal
|
18 |
4 |
3 |
25
|
|
Dudosa
|
1 |
10 |
5 |
16
|
|
Normal
|
2 |
4
|
53
|
59
|
|
Total
|
21
|
18
|
61
|
100
|
Desde un punto de vista típicamente estadístico es más adecuado liberarnos de la muestra concreta (los n ítems que son clasificados por los dos observadores) y pensar en términos de la población de la que se supone que ha sido extraída dicha muestra. La consecuencia práctica de este cambio de marco es que debemos modificar el esquema de la tabla 1 para sustituir los valores xij de cada celda por las probabilidades conjuntas, que denotaremos por Π ij (tabla 3).
| Tabla 3. Modificación del esquema de la Tabla 1 cuando se consideran probabilidades de cada resultado | |||||
|---|---|---|---|---|---|
|
Observador 2
|
|||||
|
Observador 1
|
1 |
2 |
… |
C |
Marginal
|
|
1
|
Π 11 |
Π 12 |
… |
Π 1 |
Π 1 |
|
2
|
Π 12 |
Π 22 |
… |
Π 2C |
Π 2 |
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
C
|
Π C1 |
|
|||
Con el tipo de esquematización que hemos propuesto en las tablas 1 ó 3 es evidente que las respuestas que indican concordancia son las que se sitúan sobre la diagonal principal. En efecto, si un dato se sitúa sobre dicha diagonal, ello significa que ambos observadores han clasificado el ítem en la misma categoría del sistema de clasificación. De esta observación surge naturalmente la más simple de las medidas de concordancia que consideraremos: la suma de las probabilidades a lo largo de la diagonal principal. En símbolos, si denotamos dicha medida por Π 0, será
|
|
donde los índices del sumatorio van desde i = 1 hasta i = C. |
| Como es obvio, se cumple que |
|
| correspondiendo el valor 0 a la mínima concordancia posible y el 1 a la máxima. | |
Aunque este sencillo índice ha sido propuesto en alguna ocasión como medida de concordancia de elección, su interpretación no está exenta de problemas. La tabla 4 ilustra el tipo de dificultades que pueden surgir. En el caso A, Π 0 = 0.2, luego la concordancia es mucho menor que en el caso B, donde Π 0 = 0.8. Sin embargo, condicionando por las distribuciones marginales se observa que en el caso A la concordancia es la máxima posible, mientras que en el B es la mínima.
| Tabla 4. Ejemplos de concordancia | |||||||
|---|---|---|---|---|---|---|---|
|
A |
B |
||||||
|
|
Observador 2 |
|
Observador 2 |
||||
|
Observador 1 |
1 |
2 |
Marginal |
Observador 1 |
1 |
2 |
Marginal |
|
1 |
0.1 |
0.8 |
0.9 |
1 |
0.8 |
0.1 |
0.9 |
|
2 |
0 |
0.1 |
0.1 |
2 |
0.1 |
0 |
0.1 |
|
Marginal |
0.1 |
0.9 |
1 |
Marginal |
0.9 |
0.1 |
1 |
Por lo tanto, parece claro que la búsqueda se debe orientar hacia nuevas medidas de concordancia que tengan en cuenta las distribuciones marginales, con el fin de distinguir entre dos aspectos distintos de la concordancia, a los que podríamos aludir informalmente como concordancia absoluta o relativa. El índice kappa representa una aportación en esta dirección, básicamente mediante la incorporación en su fórmula de una corrección que excluye la concordancia debida exclusivamente al azar –corrección que, como veremos, está relacionada con las distribuciones marginales–.
Con la notación ya empleada en la tabla 3, el índice kappa, Κ , se define como
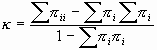 |
[1] |
| donde los índices del sumatorio van desde i = 1 hasta i = C. | |
Es instructivo analizar la expresión anterior. Observemos en primer lugar que si suponemos la independencia de las variables aleatorias que representan la clasificación de un mismo ítem por los dos observadores, entonces la probabilidad de que un ítem sea clasificado por los dos en la misma categoría i es Π i.Π .i . Por lo tanto, si extendemos el sumatorio a todas las categorías, ∑ Π i.Π .i es precisamente la probabilidad de que los dos observadores concuerden por razones exclusivamente atribuibles al azar. En consecuencia, el valor de Κ simplemente es la razón entre el exceso de concordancia observado más allá del atribuible al azar (∑ Π ii - ∑ Π i.Π .i) y el máximo exceso posible (1 - ∑ Π i.Π .i) .
La máxima concordancia posible corresponde a Κ = 1. El valor Κ = 0 se obtiene cuando la concordancia observada es precisamente la que se espera a causa exclusivamente del azar. Si la concordancia es mayor que la esperada simplemente a causa del azar, Κ > 0, mientras que si es menor, Κ < 0. El mínimo valor de Κ depende de las distribuciones marginales.
En el ejemplo de la tabla 4, Κ vale 0.024 en el caso A y -0.0216 en el B, lo que sugiere una interpretación de la concordancia opuesta a la que sugiere el índice Π 0 (vide supra). Para comprender resultados paradójicos como éstos , conviene recordar los comentarios que hacíamos más arriba acerca de las limitaciones del índice Π 0.
A la hora de interpretar el valor de Κ es útil disponer de una escala como la siguiente , a pesar de su arbitrariedad:
A partir de una muestra se puede obtener una estimación, k, del índice kappa simplemente reemplazando en la expresión [1] las probabilidades por las proporciones muestrales correspondientes:
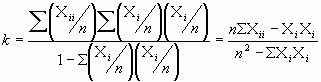 |
[2] |
Con los datos de la tabla 2 se obtiene aplicando esta fórmula un valor de k = 0.66, que según nuestra convención anterior calificaríamos como una buena concordancia.
Contrastes de hipótesis e intervalos de confianza
La obtención de una simple estimación puntual del valor de Κ no nos proporciona ninguna indicación de la precisión de dicha estimación. Desde el punto de vista de la Estadística Inferencial es esencial conocer la variabilidad de los estimadores y emplear ese conocimiento en la formulación de contrastes de hipótesis y en la construcción de intervalos de confianza.
Fleiss, Cohen y Everitt dan la expresión de la varianza asintótica –es decir, para muestras infinitamente grandes– del estimador k, cuando el verdadero valor de Κ es cero:
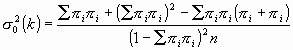 |
[3] |
Reemplazando las probabilidades teóricas, que desconocemos, por las proporciones muestrales, obtenemos un estimador de ∑ 02(k) que denotaremos por s02(k):
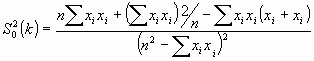 |
[4] |
Podemos emplear este resultado para contrastar la hipótesis nula de que Κ es cero frente a la alternativa de que no lo es, utilizando como estadístico del contraste el cociente
|
|
[5] |
(|k| denota el valor absoluto de k) y comparando su valor con los cuantiles de la distribución normal estándar. Con los datos de la tabla 2, k = 0.6600 y s02(k)= 0.0738, luego |k|/ s0(k)= 8.9441 y como z 0.975 = 1.96, concluimos que, al nivel de significación Δ = 0.05, el valor de k es significativo y nos lleva a rechazar que Κ sea cero.
Es discutible la utilidad del contraste de hipótesis anterior, ya que como en general es razonable esperar cierto grado de concordancia más allá del azar, nos encontraremos trivialmente con un resultado significativo. Para poder realizar contrastes de hipótesis más interesantes es necesario conocer la expresión de la varianza asintótica cuando no se supone que Κ es cero. La expresión es sensiblemente más compleja que la [3] :
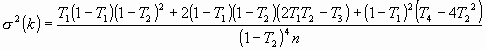 |
[6] |
| donde: |
T1 = ∑ π ii, T2 = ∑ π i.π .i, T3 = ∑ π ii(π i. + π .i), T4 = ∑ ∑ π ij(π j. + π .i)2. |
Se puede demostrar que cuando Κ es cero la expresión [6] se reduce a la [3]. Para contrastar la hipótesis nula de que Κ es igual a un valor dado Κ0 frente a una alternativa bilateral, procedemos como en el caso Κ = 0, sólo que empleando como estadístico del contraste:
|
|
[7] |
donde s(k) ahora es la raíz cuadrada de s2(k), el estimador de ∑ 2(k) obtenido sustituyendo en [6] probabilidades por proporciones muestrales. Es obvio que el caso Κ = 0 que explicábamos con anterioridad no es más que un caso particular de este contraste, con una mejor estimación del error estándar.
Volviendo al ejemplo de la tabla 2, para contrastar la hipótesis de que el verdadero valor de Κ es Κ 0 = 0.7, como k = 0.6600 y s(k) = 0.0677, calculamos |k - Κ 0|/s(k) = 0.5908 < z 0.975 = 1.96. Por tanto, al nivel de significación Δ = 0.05, no hay suficiente evidencia para rechazar la hipótesis nula.
Desde el punto de vista inferencial, un enfoque más versátil que el del contraste de hipótesis consiste en dar intervalos de confianza para el verdadero valor de Κ . Tomados simultáneamente, k y el intervalo de confianza nos dan, además de la mejor estimación de Κ , una medida del error que podemos cometer con esa estimación. Un intervalo de confianza aproximado del (1-Δ )100%, construido por el método estándar, es de la forma:
![]()
donde z 1-Δ /2 es el percentil de orden (1-Δ /2)100 de la distribución normal estándar. Con los datos de la tabla 2, nuestro intervalo de confianza del 95% para Κ sería [0.5273 , 0.7927]. Se observa como los valores 0 y 0.7 que considerábamos en los contrastes anteriores, quedan respectivamente fuera y dentro del intervalo, un hecho que ilustra la equivalencia entre los dos enfoques: contraste de hipótesis y estimación por intervalos.
Aunque el lector más interesado en los aspectos prácticos, aquél que se limita exclusivamente a usar un programa estadístico para analizar sus datos, quizás piense que todos estos detalles son algo prolijos, consideramos que son importantes para interpretar y explotar óptimamente los resultados que le brinda el programa. Por ejemplo, un programa ampliamente difundido como el SPSS, muestra solamente el valor de k (expresión [2]), su error estándar calculado a partir del estimador de [6], y el valor del estadístico [5]. Las explicaciones de este epígrafe muestran cómo utilizar estos valores para obtener intervalos de confianza y realizar otros contrastes de hipótesis.
Bibliografía
- Fleiss JL. The design and analysis of clinical experiments. New York: Wiley; 1986.
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics 1977; 33: 159-174. [Medline]
- Holley WJ, Guilford JP. A note on the G index of agreement. Educ Psychol Meas 1964; 32: 281-288.
- Bishop YMM, Fienberg SE, Holland PW. Discrete multivariate analysis: theory and practice. Cambridge, Massachussetts: MIT Press; 1977.
- Fleiss JL. Statistical methods for rates and proportions, 2nd edition. New York: Wiley; 2000.
- Feinstein AR, Cicchetti DV. High agreement but low kappa: I. The problems of two paradoxes. J Clin Epidemiol 1990; 43: 543-549. [Medline]
- Altman DG. Practical statistics for medical research. New York: Chapman and Hall; 1991.
- Fleiss JL, Cohen J, Everitt BS. Large sample standard errors of kappa and weighted kappa. Psychol Bull 1969; 72: 323-327.
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 1999; 6: 169-171.
Cálculos online
Medidas de concordancia: el índice Kappa
Índice de contenidos
Introducción
En cualquier estudio de investigación una cuestión clave es la fiabilidad de los procedimientos de medida empleados. Como señala Fleiss en el contexto de los estudios clínicos, ni el más elegante de los diseños sería capaz de paliar el daño causado por un sistema de medida poco fiable.
Tradicionalmente se ha reconocido una fuente importante de error de medida en la variabilidad entre observadores . Consecuentemente, un objetivo de los estudios de fiabilidad debe consistir en estimar el grado de dicha variabilidad.
En este sentido, dos aspectos distintos entran a formar parte típicamente del estudio de fiabilidad: de una parte, el sesgo entre observadores –dicho con menos rigor, la tendencia de un observador a dar consistentemente valores mayores que otro– y de otra, la concordancia entre observadores –es decir, hasta qué punto los observadores coinciden en su medición–.
Ciñéndonos a este segundo aspecto, la manera concreta de abordar el problema depende estrechamente de la naturaleza de los datos: si éstos son de tipo continuo es habitual la utilización de estimadores del coeficiente de correlación intraclase, mientras que cuando se trata de datos de tipo categórico el estadístico más empleado es el índice kappa, al que dedicamos el resto de este artículo.
El índice Kappa
Supongamos que dos observadores distintos clasifican independientemente una muestra de n ítems en un mismo conjunto de C categorías nominales. El resultado de esta clasificación se puede resumir en una tabla como la tabla 1, en la que cada valor xij representa el número de ítems que han sido clasificados por el observador 1 en la categoría i y por el observador 2 en la categoría j.
| Tabla 1. Formato de los datos en un estudio de concordancia | |||||
|---|---|---|---|---|---|
|
Observador 2
|
|||||
|
Observador 1
|
1 |
2 |
… |
C |
Total
|
|
1
|
X11 |
X12 |
… |
X1C |
X1 |
|
2
|
X21 |
X22 |
… |
X2C |
X2 |
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
C
|
XC1 |
XC2 |
… |
XCC |
XC |
|
Total
|
X.1 |
X.2 |
… |
X.C |
n |
Por ejemplo, podemos pensar en dos radiólogos enfrentados a la tarea de categorizar una muestra de radiografías mediante la escala: "anormal, "dudosa", "normal". La tabla 2 muestra un conjunto de datos hipotéticos para este ejemplo, dispuesto de acuerdo con el esquema de la tabla 1.
| Tabla 2. Datos hipotéticos de clasificación de una muestra de 100 radiografías por dos radiólogos | ||||
|---|---|---|---|---|
|
Radiólogo 2
|
||||
|
Radiólogo 1
|
Anormal |
Dudosa |
Normal |
Total |
|
Anormal
|
18 |
4 |
3 |
25
|
|
Dudosa
|
1 |
10 |
5 |
16
|
|
Normal
|
2 |
4
|
53
|
59
|
|
Total
|
21
|
18
|
61
|
100
|
Desde un punto de vista típicamente estadístico es más adecuado liberarnos de la muestra concreta (los n ítems que son clasificados por los dos observadores) y pensar en términos de la población de la que se supone que ha sido extraída dicha muestra. La consecuencia práctica de este cambio de marco es que debemos modificar el esquema de la tabla 1 para sustituir los valores xij de cada celda por las probabilidades conjuntas, que denotaremos por Π ij (tabla 3).
| Tabla 3. Modificación del esquema de la Tabla 1 cuando se consideran probabilidades de cada resultado | |||||
|---|---|---|---|---|---|
|
Observador 2
|
|||||
|
Observador 1
|
1 |
2 |
… |
C |
Marginal
|
|
1
|
Π 11 |
Π 12 |
… |
Π 1 |
Π 1 |
|
2
|
Π 12 |
Π 22 |
… |
Π 2C |
Π 2 |
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
.
|
.
|
· |
· |
||
|
C
|
Π C1 |
|
|||
Con el tipo de esquematización que hemos propuesto en las tablas 1 ó 3 es evidente que las respuestas que indican concordancia son las que se sitúan sobre la diagonal principal. En efecto, si un dato se sitúa sobre dicha diagonal, ello significa que ambos observadores han clasificado el ítem en la misma categoría del sistema de clasificación. De esta observación surge naturalmente la más simple de las medidas de concordancia que consideraremos: la suma de las probabilidades a lo largo de la diagonal principal. En símbolos, si denotamos dicha medida por Π 0, será
|
|
donde los índices del sumatorio van desde i = 1 hasta i = C. |
| Como es obvio, se cumple que |
|
| correspondiendo el valor 0 a la mínima concordancia posible y el 1 a la máxima. | |
Aunque este sencillo índice ha sido propuesto en alguna ocasión como medida de concordancia de elección, su interpretación no está exenta de problemas. La tabla 4 ilustra el tipo de dificultades que pueden surgir. En el caso A, Π 0 = 0.2, luego la concordancia es mucho menor que en el caso B, donde Π 0 = 0.8. Sin embargo, condicionando por las distribuciones marginales se observa que en el caso A la concordancia es la máxima posible, mientras que en el B es la mínima.
| Tabla 4. Ejemplos de concordancia | |||||||
|---|---|---|---|---|---|---|---|
|
A |
B |
||||||
|
|
Observador 2 |
|
Observador 2 |
||||
|
Observador 1 |
1 |
2 |
Marginal |
Observador 1 |
1 |
2 |
Marginal |
|
1 |
0.1 |
0.8 |
0.9 |
1 |
0.8 |
0.1 |
0.9 |
|
2 |
0 |
0.1 |
0.1 |
2 |
0.1 |
0 |
0.1 |
|
Marginal |
0.1 |
0.9 |
1 |
Marginal |
0.9 |
0.1 |
1 |
Por lo tanto, parece claro que la búsqueda se debe orientar hacia nuevas medidas de concordancia que tengan en cuenta las distribuciones marginales, con el fin de distinguir entre dos aspectos distintos de la concordancia, a los que podríamos aludir informalmente como concordancia absoluta o relativa. El índice kappa representa una aportación en esta dirección, básicamente mediante la incorporación en su fórmula de una corrección que excluye la concordancia debida exclusivamente al azar –corrección que, como veremos, está relacionada con las distribuciones marginales–.
Con la notación ya empleada en la tabla 3, el índice kappa, Κ , se define como
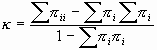 |
[1] |
| donde los índices del sumatorio van desde i = 1 hasta i = C. | |
Es instructivo analizar la expresión anterior. Observemos en primer lugar que si suponemos la independencia de las variables aleatorias que representan la clasificación de un mismo ítem por los dos observadores, entonces la probabilidad de que un ítem sea clasificado por los dos en la misma categoría i es Π i.Π .i . Por lo tanto, si extendemos el sumatorio a todas las categorías, ∑ Π i.Π .i es precisamente la probabilidad de que los dos observadores concuerden por razones exclusivamente atribuibles al azar. En consecuencia, el valor de Κ simplemente es la razón entre el exceso de concordancia observado más allá del atribuible al azar (∑ Π ii - ∑ Π i.Π .i) y el máximo exceso posible (1 - ∑ Π i.Π .i) .
La máxima concordancia posible corresponde a Κ = 1. El valor Κ = 0 se obtiene cuando la concordancia observada es precisamente la que se espera a causa exclusivamente del azar. Si la concordancia es mayor que la esperada simplemente a causa del azar, Κ > 0, mientras que si es menor, Κ < 0. El mínimo valor de Κ depende de las distribuciones marginales.
En el ejemplo de la tabla 4, Κ vale 0.024 en el caso A y -0.0216 en el B, lo que sugiere una interpretación de la concordancia opuesta a la que sugiere el índice Π 0 (vide supra). Para comprender resultados paradójicos como éstos , conviene recordar los comentarios que hacíamos más arriba acerca de las limitaciones del índice Π 0.
A la hora de interpretar el valor de Κ es útil disponer de una escala como la siguiente , a pesar de su arbitrariedad:
A partir de una muestra se puede obtener una estimación, k, del índice kappa simplemente reemplazando en la expresión [1] las probabilidades por las proporciones muestrales correspondientes:
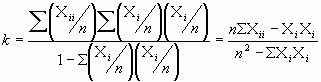 |
[2] |
Con los datos de la tabla 2 se obtiene aplicando esta fórmula un valor de k = 0.66, que según nuestra convención anterior calificaríamos como una buena concordancia.
Contrastes de hipótesis e intervalos de confianza
La obtención de una simple estimación puntual del valor de Κ no nos proporciona ninguna indicación de la precisión de dicha estimación. Desde el punto de vista de la Estadística Inferencial es esencial conocer la variabilidad de los estimadores y emplear ese conocimiento en la formulación de contrastes de hipótesis y en la construcción de intervalos de confianza.
Fleiss, Cohen y Everitt dan la expresión de la varianza asintótica –es decir, para muestras infinitamente grandes– del estimador k, cuando el verdadero valor de Κ es cero:
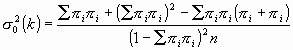 |
[3] |
Reemplazando las probabilidades teóricas, que desconocemos, por las proporciones muestrales, obtenemos un estimador de ∑ 02(k) que denotaremos por s02(k):
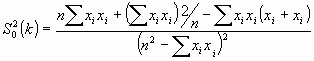 |
[4] |
Podemos emplear este resultado para contrastar la hipótesis nula de que Κ es cero frente a la alternativa de que no lo es, utilizando como estadístico del contraste el cociente
|
|
[5] |
(|k| denota el valor absoluto de k) y comparando su valor con los cuantiles de la distribución normal estándar. Con los datos de la tabla 2, k = 0.6600 y s02(k)= 0.0738, luego |k|/ s0(k)= 8.9441 y como z 0.975 = 1.96, concluimos que, al nivel de significación Δ = 0.05, el valor de k es significativo y nos lleva a rechazar que Κ sea cero.
Es discutible la utilidad del contraste de hipótesis anterior, ya que como en general es razonable esperar cierto grado de concordancia más allá del azar, nos encontraremos trivialmente con un resultado significativo. Para poder realizar contrastes de hipótesis más interesantes es necesario conocer la expresión de la varianza asintótica cuando no se supone que Κ es cero. La expresión es sensiblemente más compleja que la [3] :
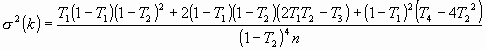 |
[6] |
| donde: |
T1 = ∑ π ii, T2 = ∑ π i.π .i, T3 = ∑ π ii(π i. + π .i), T4 = ∑ ∑ π ij(π j. + π .i)2. |
Se puede demostrar que cuando Κ es cero la expresión [6] se reduce a la [3]. Para contrastar la hipótesis nula de que Κ es igual a un valor dado Κ0 frente a una alternativa bilateral, procedemos como en el caso Κ = 0, sólo que empleando como estadístico del contraste:
|
|
[7] |
donde s(k) ahora es la raíz cuadrada de s2(k), el estimador de ∑ 2(k) obtenido sustituyendo en [6] probabilidades por proporciones muestrales. Es obvio que el caso Κ = 0 que explicábamos con anterioridad no es más que un caso particular de este contraste, con una mejor estimación del error estándar.
Volviendo al ejemplo de la tabla 2, para contrastar la hipótesis de que el verdadero valor de Κ es Κ 0 = 0.7, como k = 0.6600 y s(k) = 0.0677, calculamos |k - Κ 0|/s(k) = 0.5908 < z 0.975 = 1.96. Por tanto, al nivel de significación Δ = 0.05, no hay suficiente evidencia para rechazar la hipótesis nula.
Desde el punto de vista inferencial, un enfoque más versátil que el del contraste de hipótesis consiste en dar intervalos de confianza para el verdadero valor de Κ . Tomados simultáneamente, k y el intervalo de confianza nos dan, además de la mejor estimación de Κ , una medida del error que podemos cometer con esa estimación. Un intervalo de confianza aproximado del (1-Δ )100%, construido por el método estándar, es de la forma:
![]()
donde z 1-Δ /2 es el percentil de orden (1-Δ /2)100 de la distribución normal estándar. Con los datos de la tabla 2, nuestro intervalo de confianza del 95% para Κ sería [0.5273 , 0.7927]. Se observa como los valores 0 y 0.7 que considerábamos en los contrastes anteriores, quedan respectivamente fuera y dentro del intervalo, un hecho que ilustra la equivalencia entre los dos enfoques: contraste de hipótesis y estimación por intervalos.
Aunque el lector más interesado en los aspectos prácticos, aquél que se limita exclusivamente a usar un programa estadístico para analizar sus datos, quizás piense que todos estos detalles son algo prolijos, consideramos que son importantes para interpretar y explotar óptimamente los resultados que le brinda el programa. Por ejemplo, un programa ampliamente difundido como el SPSS, muestra solamente el valor de k (expresión [2]), su error estándar calculado a partir del estimador de [6], y el valor del estadístico [5]. Las explicaciones de este epígrafe muestran cómo utilizar estos valores para obtener intervalos de confianza y realizar otros contrastes de hipótesis.
Bibliografía
- Fleiss JL. The design and analysis of clinical experiments. New York: Wiley; 1986.
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics 1977; 33: 159-174. [Medline]
- Holley WJ, Guilford JP. A note on the G index of agreement. Educ Psychol Meas 1964; 32: 281-288.
- Bishop YMM, Fienberg SE, Holland PW. Discrete multivariate analysis: theory and practice. Cambridge, Massachussetts: MIT Press; 1977.
- Fleiss JL. Statistical methods for rates and proportions, 2nd edition. New York: Wiley; 2000.
- Feinstein AR, Cicchetti DV. High agreement but low kappa: I. The problems of two paradoxes. J Clin Epidemiol 1990; 43: 543-549. [Medline]
- Altman DG. Practical statistics for medical research. New York: Chapman and Hall; 1991.
- Fleiss JL, Cohen J, Everitt BS. Large sample standard errors of kappa and weighted kappa. Psychol Bull 1969; 72: 323-327.
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 1999; 6: 169-171.

