La distribución normal
Índice de contenidos
Introducción
Al iniciar el análisis estadístico de una serie de datos, y después de la etapa de detección y corrección de errores, un primer paso consiste en describir la distribución de las variables estudiadas y, en particular, de los datos numéricos. Además de las medidas descriptivas correspondientes, el comportamiento de estas variables puede explorarse gráficamente de un modo muy simple. Consideremos, como ejemplo, los datos de la Figura 1a, que muestra un histograma de la tensión arterial sistólica de una serie de pacientes isquémicos ingresados en una unidad de cuidados intensivos. Para construir este tipo de gráfico, se divide el rango de valores de la variable en intervalos de igual longitud, representando sobre cada intervalo un rectángulo con área proporcional al número de datos en ese rango. Uniendo los puntos medios del extremo superior de las barras, se obtiene el llamado polígono de frecuencias. Si se observase una gran cantidad de valores de la variable de interés, se podría construir un histograma en el que las bases de los rectángulos fuesen cada vez más pequeñas, de modo que el polígono de frecuencias tendría una apariencia cada vez más suavizada, tal y como se muestra en la Figura 1b. Esta curva suave "asintótica" representa de modo intuitivo la distribución teórica de la característica observada. Es la llamada función de densidad.
Una de las distribuciones teóricas mejor estudiadas en los textos de bioestadística y más utilizada en la práctica es la distribución normal, también llamada distribución gaussiana. Su importancia se debe fundamentalmente a la frecuencia con la que distintas variables asociadas a fenómenos naturales y cotidianos siguen, aproximadamente, esta distribución. Caracteres morfológicos (como la talla o el peso), o psicológicos (como el cociente intelectual) son ejemplos de variables de las que frecuentemente se asume que siguen una distribución normal. No obstante, y aunque algunos autores han señalado que el comportamiento de muchos parámetros en el campo de la salud puede ser descrito mediante una distribución normal, puede resultar incluso poco frecuente encontrar variables que se ajusten a este tipo de comportamiento.
El uso extendido de la distribución normal en las aplicaciones estadísticas puede explicarse, además, por otras razones. Muchos de los procedimientos estadísticos habitualmente utilizados asumen la normalidad de los datos observados. Aunque muchas de estas técnicas no son demasiado sensibles a desviaciones de la normal y, en general, esta hipótesis puede obviarse cuando se dispone de un número suficiente de datos, resulta recomendable contrastar siempre si se puede asumir o no una distribución normal. La simple exploración visual de los datos puede sugerir la forma de su distribución. No obstante, existen otras medidas, gráficos de normalidad y contrastes de hipótesis que pueden ayudarnos a decidir, de un modo más riguroso, si la muestra de la que se dispone procede o no de una distribución normal. Cuando los datos no sean normales, podremos o bien transformarlos o emplear otros métodos estadísticos que no exijan este tipo de restricciones (los llamados métodos no paramétricos).
A continuación se describirá la distribución normal, su ecuación matemática y sus propiedades más relevantes, proporcionando algún ejemplo sobre sus aplicaciones a la inferencia estadística. En la sección 3 se describirán los métodos habituales para contrastar la hipótesis de normalidad.
La distribución normal
La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la"campana de Gauss". La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas generalmente por ![]() y
y ![]() . Con esta notación, la densidad de la normal viene dada por la ecuación:
. Con esta notación, la densidad de la normal viene dada por la ecuación:
|
Ecuación 1: |
|
que determina la curva en forma de campana que tan bien conocemos (Figura 2). Así, se dice que una característica ![]() sigue una distribución normal de media
sigue una distribución normal de media ![]() y varianza
y varianza ![]() , y se denota como
, y se denota como ![]() , si su función de densidad viene dada por la Ecuación 1.
, si su función de densidad viene dada por la Ecuación 1.
Al igual que ocurría con un histograma, en el que el área de cada rectángulo es proporcional al número de datos en el rango de valores correspondiente si, tal y como se muestra en la Figura 2, en el eje horizontal se levantan perpendiculares en dos puntos a y b, el área bajo la curva delimitada por esas líneas indica la probabilidad de que la variable de interés, X, tome un valor cualquiera en ese intervalo. Puesto que la curva alcanza su mayor altura en torno a la media, mientras que sus "ramas" se extienden asintóticamente hacia los ejes, cuando una variable siga una distribución normal, será mucho más probable observar un dato cercano al valor medio que uno que se encuentre muy alejado de éste.
Propiedades de la distribución normal:
La distribución normal posee ciertas propiedades importantes que conviene destacar:
-
Tiene una única moda, que coincide con su media y su mediana.
-
La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre
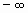 y
y 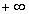 es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1. -
Es simétrica con respecto a su media
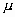 . Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
. Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor. -
La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación típica (
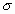 ). Cuanto mayor sea
). Cuanto mayor sea 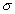 , más aplanada será la curva de la densidad.
, más aplanada será la curva de la densidad. -
El área bajo la curva comprendido entre los valores situados aproximadamente a dos desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de posibilidades de observar un valor comprendido en el intervalo
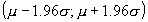 .
. -
La forma de la campana de Gauss depende de los parámetros
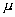 y
y 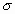 (Figura 3). La media indica la posición de la campana, de modo que para diferentes valores de
(Figura 3). La media indica la posición de la campana, de modo que para diferentes valores de 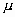 la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de
la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de 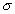 , más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
Como se deduce de este último apartado, no existe una única distribución normal, sino una familia de distribuciones con una forma común, diferenciadas por los valores de su media y su varianza. De entre todas ellas, la más utilizada es la distribución normal estándar, que corresponde a una distribución de media 0 y varianza 1. Así, la expresión que define su densidad se puede obtener de la Ecuación 1, resultando:
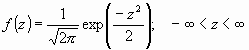
Es importante conocer que, a partir de cualquier variable X que siga una distribución ![]() , se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
, se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
|
Ecuación 2: |
|
Esta propiedad resulta especialmente interesante en la práctica, ya que para una distribución ![]() existen tablas publicadas (Tabla 1) a partir de las que se puede obtener de modo sencillo la probabilidad de observar un dato menor o igual a un cierto valor z, y que permitirán resolver preguntas de probabilidad acerca del comportamiento de variables de las que se sabe o se asume que siguen una distribución aproximadamente normal.
existen tablas publicadas (Tabla 1) a partir de las que se puede obtener de modo sencillo la probabilidad de observar un dato menor o igual a un cierto valor z, y que permitirán resolver preguntas de probabilidad acerca del comportamiento de variables de las que se sabe o se asume que siguen una distribución aproximadamente normal.
Consideremos, por ejemplo, el siguiente problema: supongamos que se sabe que el peso de los sujetos de una determinada población sigue una distribución aproximadamente normal, con una media de 80 Kg y una desviación estándar de 10 Kg. ¿Podremos saber cuál es la probabilidad de que una persona, elegida al azar, tenga un peso superior a 100 Kg?
Denotando por X a la variable que representa el peso de los individuos en esa población, ésta sigue una distribución ![]() . Si su distribución fuese la de una normal estándar podríamos utilizar la Tabla 1 para calcular la probabilidad que nos interesa. Como éste no es el caso, resultará entonces útil transformar esta característica según la Ecuación 2, y obtener la variable:
. Si su distribución fuese la de una normal estándar podríamos utilizar la Tabla 1 para calcular la probabilidad que nos interesa. Como éste no es el caso, resultará entonces útil transformar esta característica según la Ecuación 2, y obtener la variable:
![]()
para poder utilizar dicha tabla. Así, la probabilidad que se desea calcular será:
![]()
Como el área total bajo la curva es igual a 1, se puede deducir que:
![]()
Esta última probabilidad puede ser fácilmente obtenida a partir de la Tabla 1, resultando ser ![]() . Por lo tanto, la probabilidad buscada de que una persona elegida aleatoriamente de esa población tenga un peso mayor de 100 Kg , es de 1–0.9772=0.0228, es decir, aproximadamente de un 2.3%.
. Por lo tanto, la probabilidad buscada de que una persona elegida aleatoriamente de esa población tenga un peso mayor de 100 Kg , es de 1–0.9772=0.0228, es decir, aproximadamente de un 2.3%.
De modo análogo, podemos obtener la probabilidad de que el peso de un sujeto esté entre 60 y 100 Kg:
![]()
De la Figura 2, tomando a=-2 y b=2, podemos deducir que:
![]()
Por el ejemplo previo, se sabe que ![]() . Para la segunda probabilidad, sin embargo, encontramos el problema de que las tablas estándar no proporcionan el valor de
. Para la segunda probabilidad, sin embargo, encontramos el problema de que las tablas estándar no proporcionan el valor de ![]() para valores negativos de la variable. Sin embargo, haciendo uso de la simetría de la distribución normal, se tiene que:
para valores negativos de la variable. Sin embargo, haciendo uso de la simetría de la distribución normal, se tiene que:
![]()
Finalmente, la probabilidad buscada de que una persona elegida al azar tenga un peso entre 60 y 100 Kg., es de 0.9772-0.0228=0.9544, es decir, aproximadamente de un 95%. Resulta interesante comprobar que se obtendría la misma conclusión recurriendo a la propiedad (iii) de la distribución normal.
No obstante, es fácil observar que este tipo de situaciones no corresponde a lo que habitualmente nos encontramos en la práctica. Generalmente no se dispone de información acerca de la distribución teórica de la población, sino que más bien el problema se plantea a la inversa: a partir de una muestra extraída al azar de la población que se desea estudiar, se realizan una serie de mediciones y se desea extrapolar los resultados obtenidos a la población de origen. En un ejemplo similar al anterior, supongamos que se dispone del peso de n=100 individuos de esa misma población, obteniéndose una media muestral de ![]() Kg, y una desviación estándar muestral
Kg, y una desviación estándar muestral ![]() Kg, querríamos extraer alguna conclusión acerca del valor medio real de ese peso en la población original. La solución a este tipo de cuestiones se basa en un resultado elemental de la teoría estadística, el llamado teorema central del límite. Dicho axioma viene a decirnos que las medias de muestras aleatorias de cualquier variable siguen ellas mismas una distribución normal con igual media que la de la población y desviación estándar la de la población dividida por
Kg, querríamos extraer alguna conclusión acerca del valor medio real de ese peso en la población original. La solución a este tipo de cuestiones se basa en un resultado elemental de la teoría estadística, el llamado teorema central del límite. Dicho axioma viene a decirnos que las medias de muestras aleatorias de cualquier variable siguen ellas mismas una distribución normal con igual media que la de la población y desviación estándar la de la población dividida por ![]() . En nuestro caso, podremos entonces considerar la media muestral
. En nuestro caso, podremos entonces considerar la media muestral ![]() , con lo cual, a partir de la propiedad (iii) se conoce que aproximadamente un 95% de los posibles valores de
, con lo cual, a partir de la propiedad (iii) se conoce que aproximadamente un 95% de los posibles valores de ![]() caerían dentro del intervalo
caerían dentro del intervalo ![]() .
.
Puesto que los valores de ![]() y
y ![]() son desconocidos, podríamos pensar en aproximarlos por sus análogos muestrales, resultando
son desconocidos, podríamos pensar en aproximarlos por sus análogos muestrales, resultando![]() . Estaremos, por lo tanto, un 95% seguros de que el peso medio real en la población de origen oscila entre 75.6 Kg y 80.3 Kg. Aunque la teoría
. Estaremos, por lo tanto, un 95% seguros de que el peso medio real en la población de origen oscila entre 75.6 Kg y 80.3 Kg. Aunque la teoría
estadística subyacente es mucho más compleja, en líneas generales éste es el modo de construir un intervalo de confianza para la media de una población.
Contrastes de normalidad
La verificación de la hipótesis de normalidad resulta esencial para poder aplicar muchos de los procedimientos estadísticos que habitualmente se manejan. Tal y como ya se apuntaba antes, la simple exploración visual de los datos observados mediante, por ejemplo, un histograma o un diagrama de cajas, podrá ayudarnos a decidir si es razonable o no el considerar que proceden de una característica de distribución normal. Como ejemplo, consideremos los histogramas que se muestran en la Figura 4a, correspondientes a una muestra de 100 mujeres de las que se determinó su peso y edad. Para el caso del peso, la distribución se asemeja bastante a la de una normal. P ara la edad, sin embargo, es claramente asimétrica y diferente de la gaussiana.
Resulta obvio que este tipo de estudio no puede llevarnos sino a obtener una opinión meramente subjetiva acerca de la posible distribución de nuestros datos, y que es necesario disponer de otros métodos más rigurosos para contrastar este tipo de hipótesis. En primer lugar, deberemos plantearnos el saber si los datos se distribuyen de una forma simétrica con respecto a su media o presentan algún grado de asimetría, pues es ésta una de las características fundamentales de la distribución de Gauss. Aunque la simetría de la distribución pueda valorarse, de modo simple, atendiendo a algunas medidas descriptivas de la variable en cuestión (comparando, por ejemplo, los valores de media, mediana y moda), resultará útil disponer de algún índice que nos permita cuantificar cualquier desviación. Si se dispone de una muestra de tamaño n, ![]() de una característica X, se define el coeficiente de asimetría de Fisher como:
de una característica X, se define el coeficiente de asimetría de Fisher como:
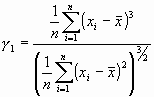
a partir del cual podemos considerar que una distribución es simétrica (![]() =0), asimétrica hacia la izquierda (
=0), asimétrica hacia la izquierda (![]() <0) o hacia la derecha (
<0) o hacia la derecha (![]() >0). En segundo lugar, podemos preguntarnos si la curva es más o menos "aplastada", en relación con el grado de apuntamiento de una distribución gaussiana. El coeficiente de aplastamiento o curtosis de Fisher, dado por:
>0). En segundo lugar, podemos preguntarnos si la curva es más o menos "aplastada", en relación con el grado de apuntamiento de una distribución gaussiana. El coeficiente de aplastamiento o curtosis de Fisher, dado por:
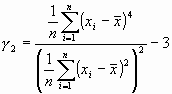
permite clasificar una distribución de frecuencias en mesocúrtica (tan aplanada como una normal, ![]() ), leptocúrtica (más apuntada que una normal,
), leptocúrtica (más apuntada que una normal, ![]() ) o platicúrtica (más aplanada que una normal,
) o platicúrtica (más aplanada que una normal, ![]() ).
).
Siguiendo con los ejemplos anteriores, y tal y como cabía esperar, el coeficiente de asimetría toma un valor mayor para la distribución de la edad (![]() ) que para el peso observado (
) que para el peso observado (![]() ). En cuanto a los niveles de curtosis, no hay apenas diferencias, siendo de –0.320 para el peso y de –0.366 para la edad.
). En cuanto a los niveles de curtosis, no hay apenas diferencias, siendo de –0.320 para el peso y de –0.366 para la edad.
Los gráficos de probabilidad normal constituyen otra importante herramienta gráfica para comprobar si un conjunto de datos puede considerarse o no procedente de una distribución normal. La idea básica consiste en enfrentar, en un mismo gráfico, los datos que han sido observados frente a los datos teóricos que se obtendrían de una distribución gaussiana. Si la distribución de la variable coincide con la normal, los puntos se concentrarán en torno a una línea recta, aunque conviene tener en cuenta que siempre tenderá a observarse mayor variabilidad en los extremos (Figura 4a, datos del peso). En los gráficos P-P se confrontan las proporciones acumuladas de una variable con las de una distribución normal. Los gráficos Q-Q se obtienen de modo análogo, esta vez representando los cuantiles respecto a los cuantiles de la distribución normal. Además de permitir valorar la desviación de la normalidad, los gráficos de probabilidad permiten conocer la causa de esa desviación. Una curva en forma de "U" o con alguna curvatura, como en el caso de la edad en la Figura 4b, significa que la distribución es asimétrica con respecto a la gaussiana, mientras que un gráfico en forma de "S" significará que la distribución tiene colas mayores o menores que la normal, esto es, que existen pocas o demasiadas observaciones en las colas de la distribución.
Parece lógico que cada uno de estos métodos se complemente con procedimientos de análisis que cuantifiquen de un modo más exacto las desviaciones de la distribución normal. Existen distintos tests estadísticos que podemos utilizar para este propósito. El test de Kolmogorov-Smirnov es el más extendido en la práctica. Se basa en la idea de comparar la función de distribución acumulada de los datos observados con la de una distribución normal, midiendo la máxima distancia entre ambas curvas. Como en cualquier test de hipótesis, la hipótesis nula se rechaza cuando el valor del estadístico supera un cierto valor crítico que se obtiene de una tabla de probabilidad. Dado que en la mayoría de los paquetes estadísticos, como el SPSS, aparece programado dicho procedimiento, y proporciona tanto el valor del test como el p-valor correspondiente, no nos detendremos más en explicar su cálculo. Existen modificaciones de este test, como el de Anderson-Darling que también pueden ser utilizados. Otro procedimiento muy extendido es también el test chi-cuadrado de bondad de ajuste. No obstante, este tipo de procedimientos deben ser utilizados con precaución. Cuando se dispone de un número suficiente de datos, cualquier test será capaz de detectar diferencias pequeñas aún cuando estas no sean relevantes para la mayor parte de los propósitos. El test de Kolmogorov-Smirnov, en este sentido, otorga un peso menor a las observaciones extremas y por la tanto es menos sensible a las desviaciones que normalmente se producen en estos tramos.
Para acabar, observemos el resultado de aplicar el test de Kolmogorov-Smirnov a los datos de la Figura 4. Para el caso del peso, el valor del estadístico proporcionado por dicho test fue de 0.705, con un p-valor correspondiente de p=0.702 que, al no ser significativo, indica que podemos asumir una distribución normal. Por otra parte, para el caso de la edad, en el que la distribución muestral era mucho más asimétrica, el mismo test proporcionó un valor de 1.498, con p=0.022, lo que obligaría a rechazar en este caso la hipótesis de una distribución gaussiana.
Más en la red
-
Normal Density Plotter (UCLA Department of Statistic)
Página que permite obtener la representación gráfica de la densidad de una distribución normal de media y desviación estándar dados por el usuario. -
SurfStat Statistical Tables - Standard Normal Distribution (University of Newcastle)
Página que permite calcular, a partir de una distribución normal estándar, la probabilidad acumulada hasta un cierto valor, o la probabilidad de tomar un valor en un intervalo. Así mismo, permite realizar los cálculos inversos, es decir, obtener el p-cuantil de una distribución normal estándar. -
Normal Density Calculator (UCLA Department of Statistic)
Permite obtener, bajo una distribución normal, la probabilidad de observar un valor mayor o igual que uno dado. La ventaja es que permite hacerlo no sólo para la distribución normal estándar, sino para valores de la media y desviación estándar dados por el usuario. -
Matt's spiffy normal plot maker (UCLA Department of Statistic)
Se introducen los datos de la variable de interes y produce el gráfico Q-Q de probabilidad normal correspondiente, que puede ser fácilmente exportado a otros programas. -
Calculation of 95% Confidence Interval on a Sample Mean (Arizona State University)
A partir del valor de la media y la desviación estándar muestral, calcula el 95% intervalo de confianza para la media poblacional.
Anexo
| Figura 4b.- Gráficos Q-Q de probabilidad. |
|---|
|
 Figura 4b 1 |
|
 Figura 4b 2 |
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 2001; 8: 268-274.
Bibliografía
- Pértega Díaz S, Pita Fernández S. Representación gráfica en el análisis de datos. Cad Aten Primaria 2001; 8: 112-117.
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
- Daniel WW. Bioestadística. Base para el análisis de las ciencias de la salud. Mexico: Limusa; 1995.
- Elston RC, Johnson WD. Essentials of Biostatistics. Philadelphia: F.A. Davis Company; 1987.
- Altman DG, Bland JM. Statistics notes: The normal distribution. BMJ 1995; 310: 298-298. [Texto completo]
- Elveback LR, Guilliver CL, Keating FR Jr. Health, Normality and the Gosth of Gauss. JAMA 1970; 211: 69-75. [Medline]
- Nelson JC, Haynes E, Willard R, Kuzma J. The Distribution of Eurhyroid Serum Protein-Bound Iodine Levels. JAMA 1971; 216: 1639-1641. [Medline]
- Altman DG, Bland JM. Statistics notes: Detecting skewness from summary information. BMJ 1996; 313: 1200-1200. [Texto completo]
- Bland JM, Altman DG. Statistics Notes: Transforming data. BMJ 1996; 312: 770. [Texto completo]
La distribución normal
Índice de contenidos
Introducción
Al iniciar el análisis estadístico de una serie de datos, y después de la etapa de detección y corrección de errores, un primer paso consiste en describir la distribución de las variables estudiadas y, en particular, de los datos numéricos. Además de las medidas descriptivas correspondientes, el comportamiento de estas variables puede explorarse gráficamente de un modo muy simple. Consideremos, como ejemplo, los datos de la Figura 1a, que muestra un histograma de la tensión arterial sistólica de una serie de pacientes isquémicos ingresados en una unidad de cuidados intensivos. Para construir este tipo de gráfico, se divide el rango de valores de la variable en intervalos de igual longitud, representando sobre cada intervalo un rectángulo con área proporcional al número de datos en ese rango. Uniendo los puntos medios del extremo superior de las barras, se obtiene el llamado polígono de frecuencias. Si se observase una gran cantidad de valores de la variable de interés, se podría construir un histograma en el que las bases de los rectángulos fuesen cada vez más pequeñas, de modo que el polígono de frecuencias tendría una apariencia cada vez más suavizada, tal y como se muestra en la Figura 1b. Esta curva suave "asintótica" representa de modo intuitivo la distribución teórica de la característica observada. Es la llamada función de densidad.
Una de las distribuciones teóricas mejor estudiadas en los textos de bioestadística y más utilizada en la práctica es la distribución normal, también llamada distribución gaussiana. Su importancia se debe fundamentalmente a la frecuencia con la que distintas variables asociadas a fenómenos naturales y cotidianos siguen, aproximadamente, esta distribución. Caracteres morfológicos (como la talla o el peso), o psicológicos (como el cociente intelectual) son ejemplos de variables de las que frecuentemente se asume que siguen una distribución normal. No obstante, y aunque algunos autores han señalado que el comportamiento de muchos parámetros en el campo de la salud puede ser descrito mediante una distribución normal, puede resultar incluso poco frecuente encontrar variables que se ajusten a este tipo de comportamiento.
El uso extendido de la distribución normal en las aplicaciones estadísticas puede explicarse, además, por otras razones. Muchos de los procedimientos estadísticos habitualmente utilizados asumen la normalidad de los datos observados. Aunque muchas de estas técnicas no son demasiado sensibles a desviaciones de la normal y, en general, esta hipótesis puede obviarse cuando se dispone de un número suficiente de datos, resulta recomendable contrastar siempre si se puede asumir o no una distribución normal. La simple exploración visual de los datos puede sugerir la forma de su distribución. No obstante, existen otras medidas, gráficos de normalidad y contrastes de hipótesis que pueden ayudarnos a decidir, de un modo más riguroso, si la muestra de la que se dispone procede o no de una distribución normal. Cuando los datos no sean normales, podremos o bien transformarlos o emplear otros métodos estadísticos que no exijan este tipo de restricciones (los llamados métodos no paramétricos).
A continuación se describirá la distribución normal, su ecuación matemática y sus propiedades más relevantes, proporcionando algún ejemplo sobre sus aplicaciones a la inferencia estadística. En la sección 3 se describirán los métodos habituales para contrastar la hipótesis de normalidad.
La distribución normal
La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la"campana de Gauss". La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas generalmente por ![]() y
y ![]() . Con esta notación, la densidad de la normal viene dada por la ecuación:
. Con esta notación, la densidad de la normal viene dada por la ecuación:
|
Ecuación 1: |
|
que determina la curva en forma de campana que tan bien conocemos (Figura 2). Así, se dice que una característica ![]() sigue una distribución normal de media
sigue una distribución normal de media ![]() y varianza
y varianza ![]() , y se denota como
, y se denota como ![]() , si su función de densidad viene dada por la Ecuación 1.
, si su función de densidad viene dada por la Ecuación 1.
Al igual que ocurría con un histograma, en el que el área de cada rectángulo es proporcional al número de datos en el rango de valores correspondiente si, tal y como se muestra en la Figura 2, en el eje horizontal se levantan perpendiculares en dos puntos a y b, el área bajo la curva delimitada por esas líneas indica la probabilidad de que la variable de interés, X, tome un valor cualquiera en ese intervalo. Puesto que la curva alcanza su mayor altura en torno a la media, mientras que sus "ramas" se extienden asintóticamente hacia los ejes, cuando una variable siga una distribución normal, será mucho más probable observar un dato cercano al valor medio que uno que se encuentre muy alejado de éste.
Propiedades de la distribución normal:
La distribución normal posee ciertas propiedades importantes que conviene destacar:
-
Tiene una única moda, que coincide con su media y su mediana.
-
La curva normal es asintótica al eje de abscisas. Por ello, cualquier valor entre
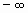 y
y 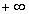 es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1. -
Es simétrica con respecto a su media
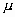 . Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
. Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor. -
La distancia entre la línea trazada en la media y el punto de inflexión de la curva es igual a una desviación típica (
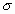 ). Cuanto mayor sea
). Cuanto mayor sea 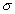 , más aplanada será la curva de la densidad.
, más aplanada será la curva de la densidad. -
El área bajo la curva comprendido entre los valores situados aproximadamente a dos desviaciones estándar de la media es igual a 0.95. En concreto, existe un 95% de posibilidades de observar un valor comprendido en el intervalo
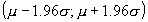 .
. -
La forma de la campana de Gauss depende de los parámetros
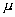 y
y 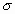 (Figura 3). La media indica la posición de la campana, de modo que para diferentes valores de
(Figura 3). La media indica la posición de la campana, de modo que para diferentes valores de 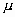 la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de
la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de 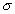 , más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
Como se deduce de este último apartado, no existe una única distribución normal, sino una familia de distribuciones con una forma común, diferenciadas por los valores de su media y su varianza. De entre todas ellas, la más utilizada es la distribución normal estándar, que corresponde a una distribución de media 0 y varianza 1. Así, la expresión que define su densidad se puede obtener de la Ecuación 1, resultando:
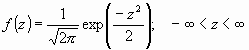
Es importante conocer que, a partir de cualquier variable X que siga una distribución ![]() , se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
, se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
|
Ecuación 2: |
|
Esta propiedad resulta especialmente interesante en la práctica, ya que para una distribución ![]() existen tablas publicadas (Tabla 1) a partir de las que se puede obtener de modo sencillo la probabilidad de observar un dato menor o igual a un cierto valor z, y que permitirán resolver preguntas de probabilidad acerca del comportamiento de variables de las que se sabe o se asume que siguen una distribución aproximadamente normal.
existen tablas publicadas (Tabla 1) a partir de las que se puede obtener de modo sencillo la probabilidad de observar un dato menor o igual a un cierto valor z, y que permitirán resolver preguntas de probabilidad acerca del comportamiento de variables de las que se sabe o se asume que siguen una distribución aproximadamente normal.
Consideremos, por ejemplo, el siguiente problema: supongamos que se sabe que el peso de los sujetos de una determinada población sigue una distribución aproximadamente normal, con una media de 80 Kg y una desviación estándar de 10 Kg. ¿Podremos saber cuál es la probabilidad de que una persona, elegida al azar, tenga un peso superior a 100 Kg?
Denotando por X a la variable que representa el peso de los individuos en esa población, ésta sigue una distribución ![]() . Si su distribución fuese la de una normal estándar podríamos utilizar la Tabla 1 para calcular la probabilidad que nos interesa. Como éste no es el caso, resultará entonces útil transformar esta característica según la Ecuación 2, y obtener la variable:
. Si su distribución fuese la de una normal estándar podríamos utilizar la Tabla 1 para calcular la probabilidad que nos interesa. Como éste no es el caso, resultará entonces útil transformar esta característica según la Ecuación 2, y obtener la variable:
![]()
para poder utilizar dicha tabla. Así, la probabilidad que se desea calcular será:
![]()
Como el área total bajo la curva es igual a 1, se puede deducir que:
![]()
Esta última probabilidad puede ser fácilmente obtenida a partir de la Tabla 1, resultando ser ![]() . Por lo tanto, la probabilidad buscada de que una persona elegida aleatoriamente de esa población tenga un peso mayor de 100 Kg , es de 1–0.9772=0.0228, es decir, aproximadamente de un 2.3%.
. Por lo tanto, la probabilidad buscada de que una persona elegida aleatoriamente de esa población tenga un peso mayor de 100 Kg , es de 1–0.9772=0.0228, es decir, aproximadamente de un 2.3%.
De modo análogo, podemos obtener la probabilidad de que el peso de un sujeto esté entre 60 y 100 Kg:
![]()
De la Figura 2, tomando a=-2 y b=2, podemos deducir que:
![]()
Por el ejemplo previo, se sabe que ![]() . Para la segunda probabilidad, sin embargo, encontramos el problema de que las tablas estándar no proporcionan el valor de
. Para la segunda probabilidad, sin embargo, encontramos el problema de que las tablas estándar no proporcionan el valor de ![]() para valores negativos de la variable. Sin embargo, haciendo uso de la simetría de la distribución normal, se tiene que:
para valores negativos de la variable. Sin embargo, haciendo uso de la simetría de la distribución normal, se tiene que:
![]()
Finalmente, la probabilidad buscada de que una persona elegida al azar tenga un peso entre 60 y 100 Kg., es de 0.9772-0.0228=0.9544, es decir, aproximadamente de un 95%. Resulta interesante comprobar que se obtendría la misma conclusión recurriendo a la propiedad (iii) de la distribución normal.
No obstante, es fácil observar que este tipo de situaciones no corresponde a lo que habitualmente nos encontramos en la práctica. Generalmente no se dispone de información acerca de la distribución teórica de la población, sino que más bien el problema se plantea a la inversa: a partir de una muestra extraída al azar de la población que se desea estudiar, se realizan una serie de mediciones y se desea extrapolar los resultados obtenidos a la población de origen. En un ejemplo similar al anterior, supongamos que se dispone del peso de n=100 individuos de esa misma población, obteniéndose una media muestral de ![]() Kg, y una desviación estándar muestral
Kg, y una desviación estándar muestral ![]() Kg, querríamos extraer alguna conclusión acerca del valor medio real de ese peso en la población original. La solución a este tipo de cuestiones se basa en un resultado elemental de la teoría estadística, el llamado teorema central del límite. Dicho axioma viene a decirnos que las medias de muestras aleatorias de cualquier variable siguen ellas mismas una distribución normal con igual media que la de la población y desviación estándar la de la población dividida por
Kg, querríamos extraer alguna conclusión acerca del valor medio real de ese peso en la población original. La solución a este tipo de cuestiones se basa en un resultado elemental de la teoría estadística, el llamado teorema central del límite. Dicho axioma viene a decirnos que las medias de muestras aleatorias de cualquier variable siguen ellas mismas una distribución normal con igual media que la de la población y desviación estándar la de la población dividida por ![]() . En nuestro caso, podremos entonces considerar la media muestral
. En nuestro caso, podremos entonces considerar la media muestral ![]() , con lo cual, a partir de la propiedad (iii) se conoce que aproximadamente un 95% de los posibles valores de
, con lo cual, a partir de la propiedad (iii) se conoce que aproximadamente un 95% de los posibles valores de ![]() caerían dentro del intervalo
caerían dentro del intervalo ![]() .
.
Puesto que los valores de ![]() y
y ![]() son desconocidos, podríamos pensar en aproximarlos por sus análogos muestrales, resultando
son desconocidos, podríamos pensar en aproximarlos por sus análogos muestrales, resultando![]() . Estaremos, por lo tanto, un 95% seguros de que el peso medio real en la población de origen oscila entre 75.6 Kg y 80.3 Kg. Aunque la teoría
. Estaremos, por lo tanto, un 95% seguros de que el peso medio real en la población de origen oscila entre 75.6 Kg y 80.3 Kg. Aunque la teoría
estadística subyacente es mucho más compleja, en líneas generales éste es el modo de construir un intervalo de confianza para la media de una población.
Contrastes de normalidad
La verificación de la hipótesis de normalidad resulta esencial para poder aplicar muchos de los procedimientos estadísticos que habitualmente se manejan. Tal y como ya se apuntaba antes, la simple exploración visual de los datos observados mediante, por ejemplo, un histograma o un diagrama de cajas, podrá ayudarnos a decidir si es razonable o no el considerar que proceden de una característica de distribución normal. Como ejemplo, consideremos los histogramas que se muestran en la Figura 4a, correspondientes a una muestra de 100 mujeres de las que se determinó su peso y edad. Para el caso del peso, la distribución se asemeja bastante a la de una normal. P ara la edad, sin embargo, es claramente asimétrica y diferente de la gaussiana.
Resulta obvio que este tipo de estudio no puede llevarnos sino a obtener una opinión meramente subjetiva acerca de la posible distribución de nuestros datos, y que es necesario disponer de otros métodos más rigurosos para contrastar este tipo de hipótesis. En primer lugar, deberemos plantearnos el saber si los datos se distribuyen de una forma simétrica con respecto a su media o presentan algún grado de asimetría, pues es ésta una de las características fundamentales de la distribución de Gauss. Aunque la simetría de la distribución pueda valorarse, de modo simple, atendiendo a algunas medidas descriptivas de la variable en cuestión (comparando, por ejemplo, los valores de media, mediana y moda), resultará útil disponer de algún índice que nos permita cuantificar cualquier desviación. Si se dispone de una muestra de tamaño n, ![]() de una característica X, se define el coeficiente de asimetría de Fisher como:
de una característica X, se define el coeficiente de asimetría de Fisher como:
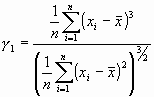
a partir del cual podemos considerar que una distribución es simétrica (![]() =0), asimétrica hacia la izquierda (
=0), asimétrica hacia la izquierda (![]() <0) o hacia la derecha (
<0) o hacia la derecha (![]() >0). En segundo lugar, podemos preguntarnos si la curva es más o menos "aplastada", en relación con el grado de apuntamiento de una distribución gaussiana. El coeficiente de aplastamiento o curtosis de Fisher, dado por:
>0). En segundo lugar, podemos preguntarnos si la curva es más o menos "aplastada", en relación con el grado de apuntamiento de una distribución gaussiana. El coeficiente de aplastamiento o curtosis de Fisher, dado por:
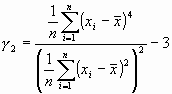
permite clasificar una distribución de frecuencias en mesocúrtica (tan aplanada como una normal, ![]() ), leptocúrtica (más apuntada que una normal,
), leptocúrtica (más apuntada que una normal, ![]() ) o platicúrtica (más aplanada que una normal,
) o platicúrtica (más aplanada que una normal, ![]() ).
).
Siguiendo con los ejemplos anteriores, y tal y como cabía esperar, el coeficiente de asimetría toma un valor mayor para la distribución de la edad (![]() ) que para el peso observado (
) que para el peso observado (![]() ). En cuanto a los niveles de curtosis, no hay apenas diferencias, siendo de –0.320 para el peso y de –0.366 para la edad.
). En cuanto a los niveles de curtosis, no hay apenas diferencias, siendo de –0.320 para el peso y de –0.366 para la edad.
Los gráficos de probabilidad normal constituyen otra importante herramienta gráfica para comprobar si un conjunto de datos puede considerarse o no procedente de una distribución normal. La idea básica consiste en enfrentar, en un mismo gráfico, los datos que han sido observados frente a los datos teóricos que se obtendrían de una distribución gaussiana. Si la distribución de la variable coincide con la normal, los puntos se concentrarán en torno a una línea recta, aunque conviene tener en cuenta que siempre tenderá a observarse mayor variabilidad en los extremos (Figura 4a, datos del peso). En los gráficos P-P se confrontan las proporciones acumuladas de una variable con las de una distribución normal. Los gráficos Q-Q se obtienen de modo análogo, esta vez representando los cuantiles respecto a los cuantiles de la distribución normal. Además de permitir valorar la desviación de la normalidad, los gráficos de probabilidad permiten conocer la causa de esa desviación. Una curva en forma de "U" o con alguna curvatura, como en el caso de la edad en la Figura 4b, significa que la distribución es asimétrica con respecto a la gaussiana, mientras que un gráfico en forma de "S" significará que la distribución tiene colas mayores o menores que la normal, esto es, que existen pocas o demasiadas observaciones en las colas de la distribución.
Parece lógico que cada uno de estos métodos se complemente con procedimientos de análisis que cuantifiquen de un modo más exacto las desviaciones de la distribución normal. Existen distintos tests estadísticos que podemos utilizar para este propósito. El test de Kolmogorov-Smirnov es el más extendido en la práctica. Se basa en la idea de comparar la función de distribución acumulada de los datos observados con la de una distribución normal, midiendo la máxima distancia entre ambas curvas. Como en cualquier test de hipótesis, la hipótesis nula se rechaza cuando el valor del estadístico supera un cierto valor crítico que se obtiene de una tabla de probabilidad. Dado que en la mayoría de los paquetes estadísticos, como el SPSS, aparece programado dicho procedimiento, y proporciona tanto el valor del test como el p-valor correspondiente, no nos detendremos más en explicar su cálculo. Existen modificaciones de este test, como el de Anderson-Darling que también pueden ser utilizados. Otro procedimiento muy extendido es también el test chi-cuadrado de bondad de ajuste. No obstante, este tipo de procedimientos deben ser utilizados con precaución. Cuando se dispone de un número suficiente de datos, cualquier test será capaz de detectar diferencias pequeñas aún cuando estas no sean relevantes para la mayor parte de los propósitos. El test de Kolmogorov-Smirnov, en este sentido, otorga un peso menor a las observaciones extremas y por la tanto es menos sensible a las desviaciones que normalmente se producen en estos tramos.
Para acabar, observemos el resultado de aplicar el test de Kolmogorov-Smirnov a los datos de la Figura 4. Para el caso del peso, el valor del estadístico proporcionado por dicho test fue de 0.705, con un p-valor correspondiente de p=0.702 que, al no ser significativo, indica que podemos asumir una distribución normal. Por otra parte, para el caso de la edad, en el que la distribución muestral era mucho más asimétrica, el mismo test proporcionó un valor de 1.498, con p=0.022, lo que obligaría a rechazar en este caso la hipótesis de una distribución gaussiana.
Más en la red
-
Normal Density Plotter (UCLA Department of Statistic)
Página que permite obtener la representación gráfica de la densidad de una distribución normal de media y desviación estándar dados por el usuario. -
SurfStat Statistical Tables - Standard Normal Distribution (University of Newcastle)
Página que permite calcular, a partir de una distribución normal estándar, la probabilidad acumulada hasta un cierto valor, o la probabilidad de tomar un valor en un intervalo. Así mismo, permite realizar los cálculos inversos, es decir, obtener el p-cuantil de una distribución normal estándar. -
Normal Density Calculator (UCLA Department of Statistic)
Permite obtener, bajo una distribución normal, la probabilidad de observar un valor mayor o igual que uno dado. La ventaja es que permite hacerlo no sólo para la distribución normal estándar, sino para valores de la media y desviación estándar dados por el usuario. -
Matt's spiffy normal plot maker (UCLA Department of Statistic)
Se introducen los datos de la variable de interes y produce el gráfico Q-Q de probabilidad normal correspondiente, que puede ser fácilmente exportado a otros programas. -
Calculation of 95% Confidence Interval on a Sample Mean (Arizona State University)
A partir del valor de la media y la desviación estándar muestral, calcula el 95% intervalo de confianza para la media poblacional.
Anexo
| Figura 4b.- Gráficos Q-Q de probabilidad. |
|---|
|
 Figura 4b 1 |
|
 Figura 4b 2 |
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña (España)
CAD ATEN PRIMARIA 2001; 8: 268-274.
Bibliografía
- Pértega Díaz S, Pita Fernández S. Representación gráfica en el análisis de datos. Cad Aten Primaria 2001; 8: 112-117.
- Altman DA. Practical statistics for medical research. 1th ed., repr. 1997. London: Chapman & Hall; 1997.
- Daniel WW. Bioestadística. Base para el análisis de las ciencias de la salud. Mexico: Limusa; 1995.
- Elston RC, Johnson WD. Essentials of Biostatistics. Philadelphia: F.A. Davis Company; 1987.
- Altman DG, Bland JM. Statistics notes: The normal distribution. BMJ 1995; 310: 298-298. [Texto completo]
- Elveback LR, Guilliver CL, Keating FR Jr. Health, Normality and the Gosth of Gauss. JAMA 1970; 211: 69-75. [Medline]
- Nelson JC, Haynes E, Willard R, Kuzma J. The Distribution of Eurhyroid Serum Protein-Bound Iodine Levels. JAMA 1971; 216: 1639-1641. [Medline]
- Altman DG, Bland JM. Statistics notes: Detecting skewness from summary information. BMJ 1996; 313: 1200-1200. [Texto completo]
- Bland JM, Altman DG. Statistics Notes: Transforming data. BMJ 1996; 312: 770. [Texto completo]

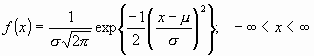



.gif)






