Determinación del tamaño muestral
Índice de contenidos
Introducción
Todo estudio epidemiológico lleva implícito en la fase de diseño la determinación del tamaño muestral necesario para la ejecución del mismo (1-4). El no realizar dicho proceso, puede llevarnos a dos situaciones diferentes: primera que realicemos el estudio sin el número adecuado de pacientes, con lo cual no podremos ser precisos al estimar los parámetros y además no encontraremos diferencias significativas cuando en la realidad sí existen. La segunda situación es que podríamos estudiar un número innecesario de pacientes, lo cual lleva implícito no solo la pérdida de tiempo e incremento de recursos innecesarios sino que además la calidad del estudio, dado dicho incremento, puede verse afectada en sentido negativo.
Para determinar el tamaño muestral de un estudio, debemos considerar diferentes situaciones (5-7):
A. Estudios para determinar parámetros. Es decir pretendemos hacer inferencias a valores poblacionales (proporciones, medias) a partir de una muestra (Tabla 1).
B. Estudios para contraste de hipótesis. Es decir pretendemos comparar si las medias o las proporciones de las muestras son diferentes.
| Tabla 1. Elementos de la Inferencia Estadística |
|---|
|
 |
Estudios para determinar parámetros
Con estos estudios pretendemos hacer inferencias a valores poblacionales (proporciones, medias) a partir de una muestra.
Si deseamos estimar una proporción, debemos saber:
- El nivel de confianza o seguridad (1-a ). El nivel de confianza prefijado da lugar a un coeficiente (Za ). Para una seguridad del 95% = 1.96, para una seguridad del 99% = 2.58.
- La precisión que deseamos para nuestro estudio.
- Una idea del valor aproximado del parámetro que queremos medir (en este caso una proporción). Esta idea se puede obtener revisando la literatura, por estudio pilotos previos. En caso de no tener dicha información utilizaremos el valor p = 0.5 (50%).
Ejemplo: ¿A cuantas personas tendríamos que estudiar para conocer la prevalencia de diabetes?
Seguridad = 95%; Precisión = 3%: Proporción esperada = asumamos que puede ser próxima al 5%; si no tuviésemos ninguna idea de dicha proporción utilizaríamos el valor p = 0,5 (50%) que maximiza el tamaño muestral:
![]()
donde:
- Za 2 = 1.962 (ya que la seguridad es del 95%)
- p = proporción esperada (en este caso 5% = 0.05)
- q = 1 – p (en este caso 1 – 0.05 = 0.95)
- d = precisión (en este caso deseamos un 3%)
![]()
Si la población es finita, es decir conocemos el total de la población y deseásemos saber cuántos del total tendremos que estudiar la respuesta seria:
![]()
donde:
- N = Total de la población
- Za2 = 1.962 (si la seguridad es del 95%)
- p = proporción esperada (en este caso 5% = 0.05)
- q = 1 – p (en este caso 1-0.05 = 0.95)
- d = precisión (en este caso deseamos un 3%).
¿A cuántas personas tendría que estudiar de una población de 15.000 habitantes para conocer la prevalencia de diabetes?
Seguridad = 95%; Precisión = 3%; proporción esperada = asumamos que puede ser próxima al 5% ; si no tuviese ninguna idea de dicha proporción utilizaríamos el valor p = 0.5 (50%) que maximiza el tamaño muestral.
![]()
Según diferentes seguridades el coeficiente de Za varía, así:
- Si la seguridad Za fuese del 90% el coeficiente sería 1.645
- Si la seguridad Za fuese del 95% el coeficiente sería 1.96
- Si la seguridad Za fuese del 97.5% el coeficiente sería 2.24
- Si la seguridad Za fuese del 99% el coeficiente sería 2.576
Si deseamos estimar una media: debemos saber:
- El nivel de confianza o seguridad (1-a ). El nivel de confianza prefijado da lugar a un coeficiente (Za ). Para una seguridad del 95% = 1.96; para una seguridad del 99% = 2.58.
- La precisión con que se desea estimar el parámetro (2 * d es la amplitud del intervalo de confianza).
- Una idea de la varianza S2 de la distribución de la variable cuantitativa que se supone existe en la población.
![]()
Ejemplo: Si deseamos conocer la media de la glucemia basal de una población, con una seguridad del 95 % y una precisión de ± 3 mg/dl y tenemos información por un estudio piloto o revisión bibliográfica que la varianza es de 250 mg/dl
![]()
Si la población es finita, como previamente se señaló, es decir conocemos el total de la población y desearíamos saber cuantos del total tendríamos que estudiar, la respuesta sería:
![]()
Estudios para contraste de hipótesis
Estos estudios pretenden comparar si las medias o las proporciones de las muestras son diferentes. Habitualmente el investigador pretende comparar dos tratamientos. Para el cálculo del tamaño muestral se precisa conocer:
- Magnitud de la diferencia a detectar que tenga interés clínicamente relevante. Se pueden comparar dos proporciones o dos medias.
- Tener una idea aproximada de los parámetros de la variable que se estudia (bibliografía, estudios previos).
- Seguridad del estudio (riesgo de cometer un error a)
- Poder estadístico (1 - b) (riesgo de cometer un error b)
- Definir si la hipótesis va a ser unilateral o bilateral.
- Bilateral: Cualquiera de los dos parámetros a comparar (medias o proporciones) puede ser mayor o menor que el otro. No se establece dirección.
- Unilateral: Cuando se considera que uno de los parámetros debe ser mayor que el otro, indicando por tanto una dirección de las diferencias.
La hipótesis bilateral es una hipótesis más conservadora y disminuye el riesgo de cometer un error de tipo I (rechazar la H0 cuando en realidad es verdadera).
B1. Comparación de dos proporciones:
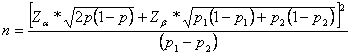
Donde:
- n = sujetos necesarios en cada una de las muestras
- Za = Valor Z correspondiente al riesgo deseado
- Zb = Valor Z correspondiente al riesgo deseado
- p1 = Valor de la proporción en el grupo de referencia, placebo, control o tratamiento habitual.
- p2 = Valor de la proporción en el grupo del nuevo tratamiento, intervención o técnica.
- p = Media de las dos proporciones p1 y p2
![]()
Los valores Za según la seguridad y Zb según el poder se indican en la Tabla 2 (8).
B2. Comparación de dos medias:
Donde:
- n = sujetos necesarios en cada una de las muestras
- Za = Valor Z correspondiente al riesgo deseado
- Zb = Valor Z correspondiente al riesgo deseado
- S2 = Varianza de la variable cuantitativa que tiene el grupo control o de referencia.
- d = Valor mínimo de la diferencia que se desea detectar (datos cuantitativos)
Los valores Za según la seguridad y Zb según el poder se indican en la Tabla 2 (8).
Ejemplo de comparación de dos medias:
Deseamos utilizar un nuevo fármaco antidiabético y consideramos que seria clínicamente eficaz si lograse un descenso de 15 mg/dl respecto al tto. Habitual con el antidiabético estándar. Por estudios previos sabemos que la desviación típica de la glucemia en pacientes que reciben el tratamiento habitual es de 16 mg/dl. Aceptamos un riesgo de 0.05 y deseamos un poder estadístico de 90% para detectar diferencias si es que existen.
precisamos 20 pacientes en cada grupo.
Ejemplo de comparación de dos proporciones:
Deseamos evaluar si el Tratamiento T2 es mejor que el tratamiento T1 para el alivio del dolor para lo que diseñamos un ensayo clínico. Sabemos por datos previos que la eficacia del fármaco habitual está alrededor del 70% y consideramos clínicamente relevante si el nuevo fármaco alivia el dolor en un 90%. Nuestro nivel de riesgo lo fijamos en 0.05 y deseamos un poder estadístico de un 80%.
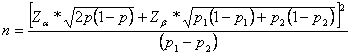
![]()
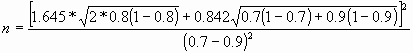
n = 48 pacientes. En cada grupo precisamos 48 pacientes.
El tamaño muestral ajustado a las pérdidas:
En todos los estudios es preciso estimar las posibles perdidas de pacientes por razones diversas (pérdida de información, abandono, no respuesta….) por lo que se debe incrementar el tamaño muestral respecto a dichas pérdidas.
El tamaño muestral ajustado a las pérdidas se puede calcular:
Muestra ajustada a las pérdidas = n (1 / 1–R)
- n = número de sujetos sin pérdidas
- R = proporción esperada de pérdidas
Así por ejemplo si en el estudio anterior esperamos tener un 15% de pérdidas el tamaño muestral necesario seria: 48 (1 / 1-0.15) = 56 pacientes en cada grupo.
Cálculos online
Bibliografía
- Contandriopoulos AP, Champagne F, Potvin L, Denis JL, Boyle P. Preparar un proyecto de investigación. Barcelona: SG Editores ; 1991.
- Hulley SB, Cummings SR. Diseño de la investigación clínica. Un enfoque epidemiológico. Barcelona: Doyma; 1993.
- Cook TD., Campbell DT. Quasi-Experimentation. Design & Analysis Issues for Field Settings. Boston: Houghton Mifflin Company; 1979.
- Kleinbaum DG., Kupper LL., Morgenstern H. Epidemiologic Research. Principles and Quantitative Methods. Belmont, California: Lifetime Learning Publications. Wadsworth; 1982.
- Dawson-Saunders B, Trapp RG. Bioestadística Médica . 2ª ed. México: Editorial el Manual Moderno; 1996.
- Milton JS, Tsokos JO. Estadística para biología y ciencias de la salud. Madrid: Interamericana McGraw Hill; 2001.
- Martín Andrés A, Luna del Castillo JD. Bioestadística para las ciencias de la salud. 4ª ed. Madrid: NORMA; 1993.
- Argimón Pallas J.M., Jiménez Villa J. Métodos de investigación aplicados a la atención primaria de salud. 2ª ed. Barcelona: Mosby-Doyma; 1994
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña
CAD ATEN PRIMARIA 1996; 3: 138-14.
Determinación del tamaño muestral
Índice de contenidos
Introducción
Todo estudio epidemiológico lleva implícito en la fase de diseño la determinación del tamaño muestral necesario para la ejecución del mismo (1-4). El no realizar dicho proceso, puede llevarnos a dos situaciones diferentes: primera que realicemos el estudio sin el número adecuado de pacientes, con lo cual no podremos ser precisos al estimar los parámetros y además no encontraremos diferencias significativas cuando en la realidad sí existen. La segunda situación es que podríamos estudiar un número innecesario de pacientes, lo cual lleva implícito no solo la pérdida de tiempo e incremento de recursos innecesarios sino que además la calidad del estudio, dado dicho incremento, puede verse afectada en sentido negativo.
Para determinar el tamaño muestral de un estudio, debemos considerar diferentes situaciones (5-7):
A. Estudios para determinar parámetros. Es decir pretendemos hacer inferencias a valores poblacionales (proporciones, medias) a partir de una muestra (Tabla 1).
B. Estudios para contraste de hipótesis. Es decir pretendemos comparar si las medias o las proporciones de las muestras son diferentes.
| Tabla 1. Elementos de la Inferencia Estadística |
|---|
|
 |
Estudios para determinar parámetros
Con estos estudios pretendemos hacer inferencias a valores poblacionales (proporciones, medias) a partir de una muestra.
Si deseamos estimar una proporción, debemos saber:
- El nivel de confianza o seguridad (1-a ). El nivel de confianza prefijado da lugar a un coeficiente (Za ). Para una seguridad del 95% = 1.96, para una seguridad del 99% = 2.58.
- La precisión que deseamos para nuestro estudio.
- Una idea del valor aproximado del parámetro que queremos medir (en este caso una proporción). Esta idea se puede obtener revisando la literatura, por estudio pilotos previos. En caso de no tener dicha información utilizaremos el valor p = 0.5 (50%).
Ejemplo: ¿A cuantas personas tendríamos que estudiar para conocer la prevalencia de diabetes?
Seguridad = 95%; Precisión = 3%: Proporción esperada = asumamos que puede ser próxima al 5%; si no tuviésemos ninguna idea de dicha proporción utilizaríamos el valor p = 0,5 (50%) que maximiza el tamaño muestral:
![]()
donde:
- Za 2 = 1.962 (ya que la seguridad es del 95%)
- p = proporción esperada (en este caso 5% = 0.05)
- q = 1 – p (en este caso 1 – 0.05 = 0.95)
- d = precisión (en este caso deseamos un 3%)
![]()
Si la población es finita, es decir conocemos el total de la población y deseásemos saber cuántos del total tendremos que estudiar la respuesta seria:
![]()
donde:
- N = Total de la población
- Za2 = 1.962 (si la seguridad es del 95%)
- p = proporción esperada (en este caso 5% = 0.05)
- q = 1 – p (en este caso 1-0.05 = 0.95)
- d = precisión (en este caso deseamos un 3%).
¿A cuántas personas tendría que estudiar de una población de 15.000 habitantes para conocer la prevalencia de diabetes?
Seguridad = 95%; Precisión = 3%; proporción esperada = asumamos que puede ser próxima al 5% ; si no tuviese ninguna idea de dicha proporción utilizaríamos el valor p = 0.5 (50%) que maximiza el tamaño muestral.
![]()
Según diferentes seguridades el coeficiente de Za varía, así:
- Si la seguridad Za fuese del 90% el coeficiente sería 1.645
- Si la seguridad Za fuese del 95% el coeficiente sería 1.96
- Si la seguridad Za fuese del 97.5% el coeficiente sería 2.24
- Si la seguridad Za fuese del 99% el coeficiente sería 2.576
Si deseamos estimar una media: debemos saber:
- El nivel de confianza o seguridad (1-a ). El nivel de confianza prefijado da lugar a un coeficiente (Za ). Para una seguridad del 95% = 1.96; para una seguridad del 99% = 2.58.
- La precisión con que se desea estimar el parámetro (2 * d es la amplitud del intervalo de confianza).
- Una idea de la varianza S2 de la distribución de la variable cuantitativa que se supone existe en la población.
![]()
Ejemplo: Si deseamos conocer la media de la glucemia basal de una población, con una seguridad del 95 % y una precisión de ± 3 mg/dl y tenemos información por un estudio piloto o revisión bibliográfica que la varianza es de 250 mg/dl
![]()
Si la población es finita, como previamente se señaló, es decir conocemos el total de la población y desearíamos saber cuantos del total tendríamos que estudiar, la respuesta sería:
![]()
Estudios para contraste de hipótesis
Estos estudios pretenden comparar si las medias o las proporciones de las muestras son diferentes. Habitualmente el investigador pretende comparar dos tratamientos. Para el cálculo del tamaño muestral se precisa conocer:
- Magnitud de la diferencia a detectar que tenga interés clínicamente relevante. Se pueden comparar dos proporciones o dos medias.
- Tener una idea aproximada de los parámetros de la variable que se estudia (bibliografía, estudios previos).
- Seguridad del estudio (riesgo de cometer un error a)
- Poder estadístico (1 - b) (riesgo de cometer un error b)
- Definir si la hipótesis va a ser unilateral o bilateral.
- Bilateral: Cualquiera de los dos parámetros a comparar (medias o proporciones) puede ser mayor o menor que el otro. No se establece dirección.
- Unilateral: Cuando se considera que uno de los parámetros debe ser mayor que el otro, indicando por tanto una dirección de las diferencias.
La hipótesis bilateral es una hipótesis más conservadora y disminuye el riesgo de cometer un error de tipo I (rechazar la H0 cuando en realidad es verdadera).
B1. Comparación de dos proporciones:
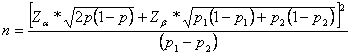
Donde:
- n = sujetos necesarios en cada una de las muestras
- Za = Valor Z correspondiente al riesgo deseado
- Zb = Valor Z correspondiente al riesgo deseado
- p1 = Valor de la proporción en el grupo de referencia, placebo, control o tratamiento habitual.
- p2 = Valor de la proporción en el grupo del nuevo tratamiento, intervención o técnica.
- p = Media de las dos proporciones p1 y p2
![]()
Los valores Za según la seguridad y Zb según el poder se indican en la Tabla 2 (8).
B2. Comparación de dos medias:
Donde:
- n = sujetos necesarios en cada una de las muestras
- Za = Valor Z correspondiente al riesgo deseado
- Zb = Valor Z correspondiente al riesgo deseado
- S2 = Varianza de la variable cuantitativa que tiene el grupo control o de referencia.
- d = Valor mínimo de la diferencia que se desea detectar (datos cuantitativos)
Los valores Za según la seguridad y Zb según el poder se indican en la Tabla 2 (8).
Ejemplo de comparación de dos medias:
Deseamos utilizar un nuevo fármaco antidiabético y consideramos que seria clínicamente eficaz si lograse un descenso de 15 mg/dl respecto al tto. Habitual con el antidiabético estándar. Por estudios previos sabemos que la desviación típica de la glucemia en pacientes que reciben el tratamiento habitual es de 16 mg/dl. Aceptamos un riesgo de 0.05 y deseamos un poder estadístico de 90% para detectar diferencias si es que existen.
precisamos 20 pacientes en cada grupo.
Ejemplo de comparación de dos proporciones:
Deseamos evaluar si el Tratamiento T2 es mejor que el tratamiento T1 para el alivio del dolor para lo que diseñamos un ensayo clínico. Sabemos por datos previos que la eficacia del fármaco habitual está alrededor del 70% y consideramos clínicamente relevante si el nuevo fármaco alivia el dolor en un 90%. Nuestro nivel de riesgo lo fijamos en 0.05 y deseamos un poder estadístico de un 80%.
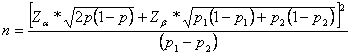
![]()
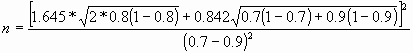
n = 48 pacientes. En cada grupo precisamos 48 pacientes.
El tamaño muestral ajustado a las pérdidas:
En todos los estudios es preciso estimar las posibles perdidas de pacientes por razones diversas (pérdida de información, abandono, no respuesta….) por lo que se debe incrementar el tamaño muestral respecto a dichas pérdidas.
El tamaño muestral ajustado a las pérdidas se puede calcular:
Muestra ajustada a las pérdidas = n (1 / 1–R)
- n = número de sujetos sin pérdidas
- R = proporción esperada de pérdidas
Así por ejemplo si en el estudio anterior esperamos tener un 15% de pérdidas el tamaño muestral necesario seria: 48 (1 / 1-0.15) = 56 pacientes en cada grupo.
Cálculos online
Bibliografía
- Contandriopoulos AP, Champagne F, Potvin L, Denis JL, Boyle P. Preparar un proyecto de investigación. Barcelona: SG Editores ; 1991.
- Hulley SB, Cummings SR. Diseño de la investigación clínica. Un enfoque epidemiológico. Barcelona: Doyma; 1993.
- Cook TD., Campbell DT. Quasi-Experimentation. Design & Analysis Issues for Field Settings. Boston: Houghton Mifflin Company; 1979.
- Kleinbaum DG., Kupper LL., Morgenstern H. Epidemiologic Research. Principles and Quantitative Methods. Belmont, California: Lifetime Learning Publications. Wadsworth; 1982.
- Dawson-Saunders B, Trapp RG. Bioestadística Médica . 2ª ed. México: Editorial el Manual Moderno; 1996.
- Milton JS, Tsokos JO. Estadística para biología y ciencias de la salud. Madrid: Interamericana McGraw Hill; 2001.
- Martín Andrés A, Luna del Castillo JD. Bioestadística para las ciencias de la salud. 4ª ed. Madrid: NORMA; 1993.
- Argimón Pallas J.M., Jiménez Villa J. Métodos de investigación aplicados a la atención primaria de salud. 2ª ed. Barcelona: Mosby-Doyma; 1994
Autores
Unidad de Epidemiología Clínica y Bioestadística. Complexo Hospitalario Universitario de A Coruña
CAD ATEN PRIMARIA 1996; 3: 138-14.

